지난 시간까지 테브난의 정리에 대해서
배워봤습니다.
오늘은 노턴의 정리를 배울겁니다.
노턴의 정리는 사실 테브난 정리와 같습니다.
다만.
어느 관점에서 회로를 바라보느냐의 차이입니다.

자.
이게 무슨이야기이냐면.
이미 지난포스팅에서 테브난의 정리에
대해서 아래와 같이 정의했었는데요.
'두개의 선형 회로가
전압원(단자의 개방회로 전압)과 저항(독립 전원 off 상태에서의 등가저항)이
직렬로 연결된 등가회로로
대체될 수 있다'
라고 이야기했었죠?
노턴의 정리는. 이렇습니다.
'두개의 선형 회로가
전류원(단락회로 종단에 흐르는 전류)과 저항(독립 전원 off 상태에서의 등가저항)이
병렬로 연결된 등가회로로
대체될 수 있다'
차이점을 보아하니
전압원이 아니라 전류원이라는점.
직렬이 아니라 병렬이라는 점이 다른 것 같습니다.
이해를 돕기위해서
지난포스팅에 사용했던 그림을 그대로 설명해드리는 것이 이해가 빠르겠네요

테브난 등가회로가 선형성을 만족해야 성립되듯이
노턴의정리 역시 선형성을 만족해야 성립됩니다.
아래그림은 테브난 등가회로를 설명하면서 나타냈었던
지난포스팅의 자료를 인용한건데요.

테브난의 정리를 설명했을 당시에는
그림 1이
아래와 같이 표현되었었죠.

노턴의 정리는 어떻게 표현될까요?
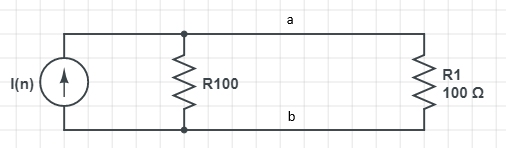
사실상.
전압원이 전류원으로 바뀌었고.
저항이 직렬연결에서 병렬연결로 바뀌었다는 점외에
모두 동일합니다.
이는...
가만히 생각해보면.
앞선 포스팅에서 언급했던 전원변환 챕터와
동일한 의미를 가집니다.
그렇담...
어떻게 노턴의 등가저항과
노턴의 등가 전류원을 구할 수 있느냐?
사실 노턴의 등가저항은.
앞에서 언급했던 포스팅과 완전히 동일한 방법으로 구할 수 있습니다.
이전 포스팅을 찾아가기 힘드신 분들을 위해서
지난 포스팅을 그대로 인용하겠습니다.
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ 테브난의 등가저항 구하기(포스팅 인용)글 ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
STEP 2 노턴의 등가저항 구하기
등가저항을 구하는 방법은 조금 까다로울 수 있겠네요.
먼저, R1을 떼버리고 생각하는 것도 동일합니다.
R1이 영향을 끼지지 않도록 한뒤 나머지가 어떻게 변화하는지를 확인하고 싶은거니까요.
헌데... 경우가 2가지로 나뉩니다.
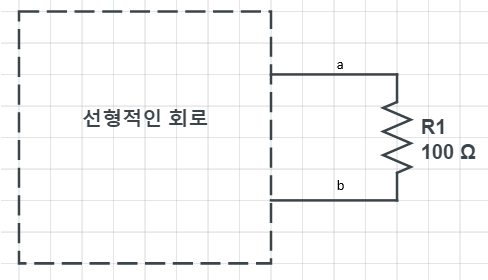
선형적인 회로라고 표기되어 있는부분에
종속 전원을 가지고 있느냐 아니냐.
종속전원을 가지고 있지 않다면
단순히 독립전원을 꺼버리고(꺼버린다는 의미는 독립전원을 없애고 단락상태로 만든다는 의미) a, b를
멀티미터로 찍어서 V(th)를 구하면 됩니다.
종속전원을 가지고 있는 경우에는
종속전원을 제외한 독립전원을 다꺼버린뒤
외부에서 전압을 1[V]를 인가하는 방법을 생각 할 수 있는데
이게 무슨 의미인지 헷갈릴 수 있어 설명을 추가합니다.
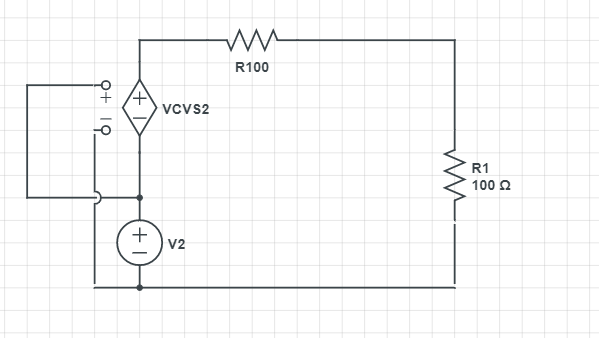
먼저 위와 같은 회로가
주어졌다면.
R1은 부하측이니 일단 제거합니다.
그렇담
아래 그림처럼 되겠지요?

이때 양 개방단자를 멀티미터로 찍는데
그전에 V2를 끄고 단락상태로 만든다음
마찬가지로 VCVS2도 꺼야 마땅하나
문제는 VCVS2가 외부요인에 종속되어 골치가 아픈경우입니다.
결과론적으로 보면
위 그림같은 경우야 V2에 종속되어 사실상 꺼버려도 무관하겠지만
우리는 실제로 선형적인 회로가 어떻게 생겼는지 일일히 관찰하기도 어려울 뿐더러
어떤 변수가 서로 얽히고 섥혀있는지 알기도 힘듭니다.
해서 편법을 씁니다.
아래 그림에서

V2만 꺼버리고 VCVS2는 냅둔 상태에서
외부에서 1[V] 전압원을 인가하는 겁니다.
그리고 a 단자쪽으로 들어가는 전류를 I(o)로 두어
전류를 구하여
1[V] 외부전압원 / I(o) 멀티테스터기 측정전류치 = R(th)
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
STEP 1 노턴의 등가회로 단락전류 구하기
사실. 단락전류 구하는 방법은 너무쉽습니다.
왜냐하면

위 회로에서 R1을 날리면
필시

여기서 a, b를 단락시켰다고 가정했을때 전류가 바로
노턴의 정리
등가전류입니다.
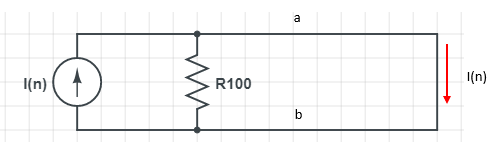
당연히 I(n)이 흐를 수 밖에 없을겁니다.
여기서.
V(테브난 등가전압) = R(테브난 등가저항 or 노턴의 등가저항) * I(노턴 전류 = 단락전류)
와 같은 관계식이 성립하는데
이는 테브난 등가회로와 노턴의 정리가 서로
전원변환 관계에 의해 자유자재로 변환될 수 있음을 암시하죠
노턴의 정리던 테브난 등가회로던 실상 실무에서
이러한 이론이 많이 쓰이지는 않는거 같습니다.

박사급 엔지니어로써 새로운 회로를 개발하거나 연구소에 있지 않는이상
우리는 누군가 잘만들어 놓은 것을 활용하기만 하면 되니까요.
허나 이론을 알고서 실무를 접근하는 것과
이론에 전무하고 실무를 접근하는 것에는 분명한 차이가 있습니다.
제 경험상...
이론을 알고 있는 후배들이 조금더 이해도라든가 업무 습득 속도가 월등히 우수했던 것 같습니다.
여러분도.
쓸데없는 공부라고 생각하지 마시고...
목적을 가지고 공부를 해보시기 바랍니다.
'전기공학 기초이론 > 회로이론' 카테고리의 다른 글
| [회로이론] - 연산증폭기 OP AMP란 무엇인가? - 개요2 (0) | 2022.01.15 |
|---|---|
| [회로이론] - 연산증폭기 OP AMP란 무엇인가? - 개요1 (0) | 2022.01.04 |
| [회로이론] - 테브난의 정리 예제 (1) | 2021.12.20 |
| [회로이론] - 테브난 정리 (0) | 2021.12.06 |
| [회로이론] - 전원을 변환해서 회로를 해석할 수 있다고? (0) | 2021.07.18 |



