'테브난'에 해당되는 글 2건

지난시간에 이어서

 

테브난의 예제에 대해서 살펴보는 시간을

 

가져보고 짧게 끝내보겠습니다.

 

---

 

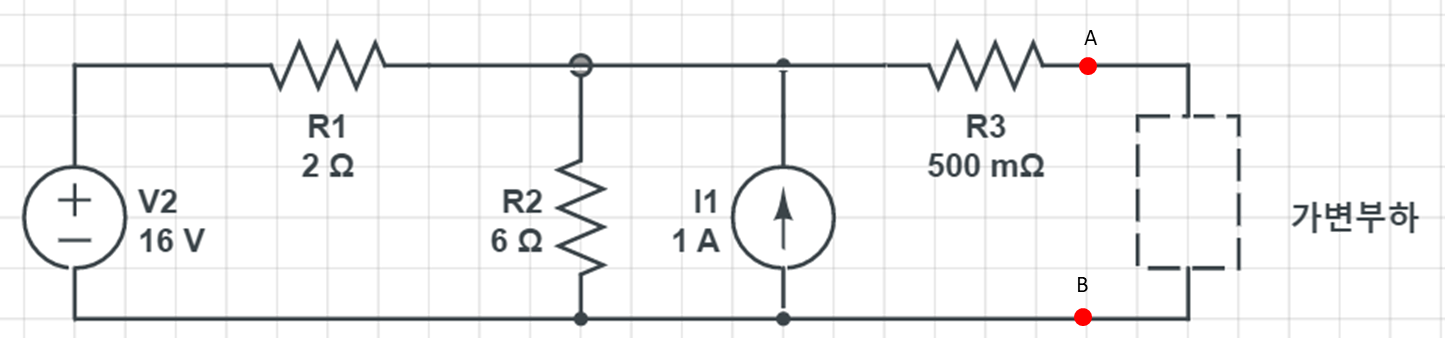
문제는 이렇습니다.

 

QUEST NO. 1

 

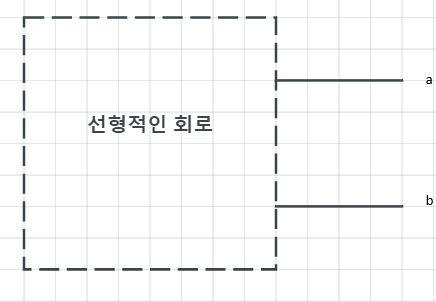
A, B단자 기준으로

 

왼쪽의 테브난 등가회로를 구해봅시다.

 

지난시간에 말씀드렸다시피 2가지

 

규칙이 있었죠?

 

기억 안나시는분은 지난번 포스팅 다시 참고해보시길...

 

아참.

 

이회로를 들어가기전에 먼저 따져야 하는게 있었죠?

 

선형성을 만족하느냐에요.

 

보시다시피 이상적인 전압원, 전류원

 

저항으로만 이루어진 위 두 회로는 모두 선형성을 만족합니다.

 

여기서 두회로란...

 

이상, 2가지 회로를 뜻하는데

 

두회로는 모두 선형성을 만족한다는 사실을 쉽게 알 수 있을겁니다.

 

테브난 등가회로가 선형성을 가지는 두회로가 하나의 회로로 변환된다는 사실을

 

알았을 경우

 

위 회로는 테브난 등가회로로 변환 가능함을 암시하는데..

 

이제...

 

 

본격적으로 문제를 해결해봅시다.

 

먼저

 

테브난 등가저항을 먼저 구해보겠습니다.

 

테브난 등가저항을 구할때는 먼저...

 

이상적인 독립전원을 끄라고 말씀드렸었죠?

 

끄라는 것의 의미는

 

이상적인 전압원은 단락시켜버리고

 

이상적인 전류원은 개방시켜버리는 것을

 

의미합니다.

 

 

외우지 마시고 잘 생각해보시면 압니다.

 

위 회로에서 끄다의 본질적의 의미는 아마도...

 

 '회로 구실을 못하게 만들어버려라' 일 것입니다

 

전압원이 회로구실을 못하게 만들려면 전압원 양단을

 

디지털멀티미터로 측정하였을때 0[V] 가 찍혀야겠죠?

 

이는. 바꾸어 말하면

 

단락회로와 동일합니다

 

전류원이 회로구실을 못하게 만들려면 전류원 양단을

 

디지털멀티미터로 측정하였을때 0[A] 가 찍혀야겠죠?

 

이는. 바꾸어 말하면

 

개방회로와 동일하죠.

 

이렇게 두회로의 전압원과 전류원을 끄게되면

 

아래와 같은 회로가 만들어집니다.

 

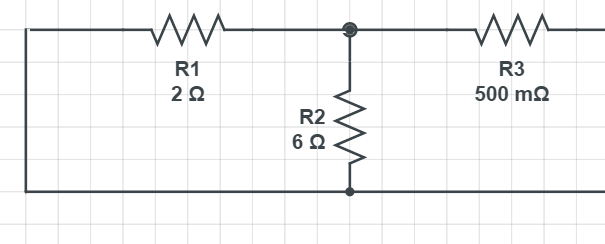
위 회로에서 등가 저항을 구하는 방법은

 

우리가 이전포스팅에서 배웠던 합성저항 공식과 동일합니다.

 

 

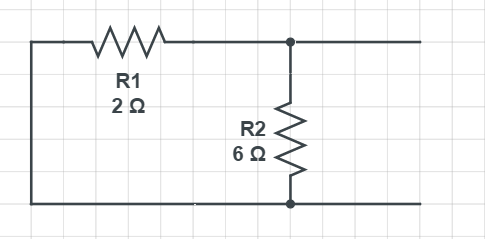
먼저 R1과 R2는 병렬회로이므로

 

1 / (1/2 + 1/6) = R1과 R2의 합성저항

 

즉,

 

R1과 R2의 합성저항이 1.5 [OHM]

 

나온다는 사실을 쉽게 구할 수 있고,

 

 

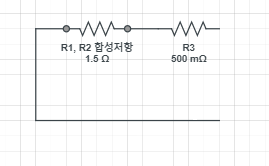
마찬가지로 R1 R2의 합성저항 1.5 [OHM]과 R3 0.5 [OHM]이

 

직렬연결 되어있으므로

 

R1 R2 R3의 총합성저항이 2 [OHM]이 된다는 사실을 알 수 있습니다.

 

즉 테브난 등가저항은 2 [OHM] 입니다.

 

 

 

 

그렇담 테브난 등가 전압은 어떻게 구해야 할까요???

 

 

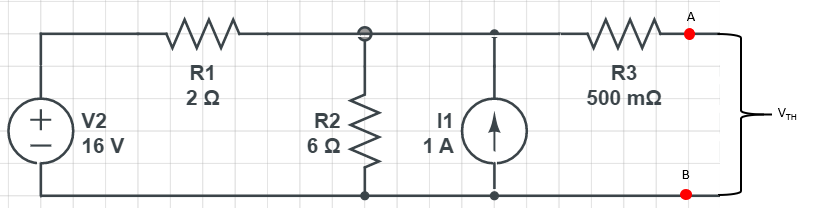
먼저...

 

테브난 등가전압이라 함은

 

가변부하단을 제외한 A, B 단자의 왼쪽 회로 전압을 측정한 것이죠.

 

위회로가 이상적인 소자 및 전원만 사용한다고 가정하면 회로 A는

 

아래 회로 B처럼 대체될 수 있습니다.

 

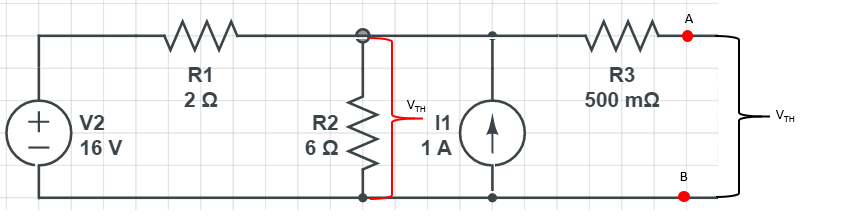
그 이유인 즉슨

 

이상적인 전류원은 저항이 엄청나게 크기 때문에

 

실상 개방회로와 같기 때문이죠.

 

여기서 V(th)를 구하는건 식은죽 먹기입니다.

 

왜냐면...

 

이미 앞선 포스팅에서 수많은 강의를 해왔기 때문.

 

회로B의 각각 루프에 메시를 돌려봅시다.

 

 

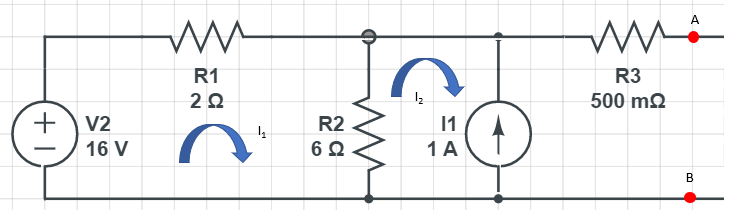
먼저

 

 

 

-16 + 2 * I1 +6 * (I1 - I2) = 0 ∙∙∙∙ 1번 수식

 

1번수식을 정리해보면.

 

8 * I1 - 6 * I2 = 16

 

I2 = -1[A] ∙∙∙∙ 2번수식

 

식을 정리해보면

 

I1 =  1.25[A] 임을 알 수 있음.

 

즉 

Vth는

 

6* ( 1.25 + 1 ) = 13.5[V]

 

라는 사실.

 

정리하면

 

테브난 등가회로는

 

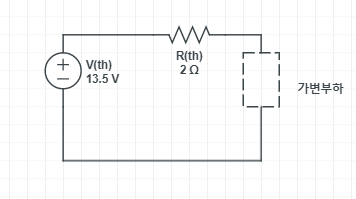
이렇게 구한 테브난 등가회로는 이렇게 쓰입니다.

 

실제로 가변부하는

 

 

냉장고가 될 수도 있고

 

세탁기가 될 수도 있겠죠.

 

테브난 등가회로로 나타냈으니 망정이지

 

이거를 이렇게 나타낸다면 얼마나 힘들겠어요???

 

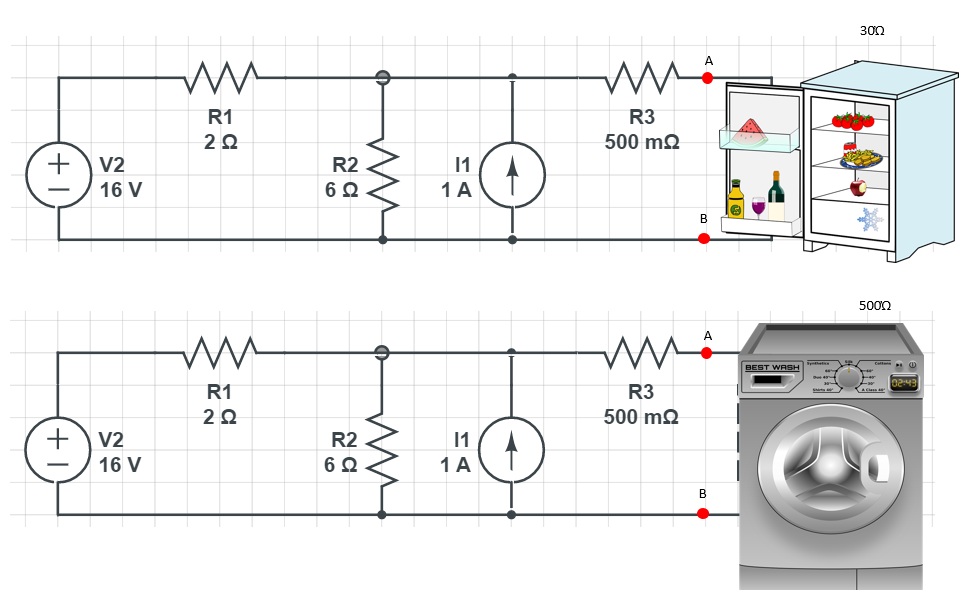
부하가 바뀔때마다 매번 새로운 회로를 해석해야 하니 말입니다.

 

무슨이야긴지 충분히 이해하셨으리라 봅니다.

 

오늘 정신이 없는 상태에서 급하게 포스팅하다보니

 

계산실수가 있는가 모르겠네요..

 

무튼 언제든지 문제에 대한 피드백은 환영입니다.

 

오늘은 여기까지 할게요.

이론을 소개하기 이전

 

앞서 개요에 대해서 설명했었습니다.

 

오늘은 바로 이론적인 부분을 공부해보도록 할까요?

 

테브난 정리는

 

간단하게 말하자면

 

두개의 선형 회로가

 

전압원(단자의 개방회로 전압)과 저항(독립 전원 off 상태에서의 등가저항)이

 

직렬로 연결된 등가회로로

 

대체될 수 있다는 것을 뜻합니다.

 

 

자.

 

당연히 이렇게 말하면 이해하기 어렵습니다.

 

전기를 전공한 제게도 어렵고

 

말을 곧이곧대로 이해해서는 결코 이해가 되지 않는 것이 사실이죠.

 

이런 경우에 쉽게 이해할 수 있도록

 

전공 서적에 그림과 함께 자세한 사례가 표현되면

 

이해하기 더할나위 없이 좋을텐데....

 

너무 자세히 나와있어서 뭘 포인트로 집어야 하는지 알쏭달쏭하기도 하고

 

말이 너무 어려워서 이해하기를 금방 포기해버리죠.

 

저는 회로이론을 공부한지 약 10년이 지났지만

 

최대한 학생이었을때 입장으로 쉽게 작성해보겠습니다.

 

---

 

선형회로가 뭔지는 귀에 딱지 박혔을 정도로 말씀드렸던 것 같으니

 

가볍게 패스하겠습니다.

 

중요한건.

 

테브난 등가회로는 선형회로에만 적용이 될 수 있다는 점을

 

반드시

 

반드시

 

반드시

 

이해하여야 한다는 사실

 

위 그림에 표시한 선형적인 회로는

 

무엇이냐?

 

간단합니다.

 

이상적인 저항과 전압원의 회로조합이라고 보시면 되겠고...

 

네... 현실에는 없는 전기입니다.

 

하지만 효용가치가 아예 없지는 않아요.

 

공학은 수학과 달라서 수식으로부터 실제와 비슷한 값을 얻어내는 것이 의미가 있거든요.

 

주의할점은

 

전력을 계산할때 우리는

 

P = I^2 * R 의 꼴로

 

많이 표시하죠?

 

전력은 보시다시피 2차함수로 비선형 회로에 속합니다.

 

한마디로.

 

테브난 등가회로는 전력공학에서는 통하지 않는다.

 

이걸 아는게 매우매우 중요합니다.

 

 

대학생때 어떻게든 좋은 학점받으려고 기초가 흔들리는 상태에서

 

지식만 쌓으니 결국은 돌아돌아 다시 기초를 찾아가는데

 

시간을 너무 많이 낭비했어요.

 

제발 그러지 마시길 당부드립니다.

 

실무자가 된 지금에서도 회로이론 전공 교과서는 늘 새롭더라구요.

 

---

테브난 등가회로를 공부하는 목적

 

복잡한 회로를 간략화하여 문제해결을 쉽게하기 위함.

 

목적을 머리속에 콕박은뒤 어떤식으로

 

복잡한 회로가 간단하게 표현된다는 것인지 보겠습니다. 

 

어쨋든 위 회로에

 

양단자 a, b에다가

 

부하를 붙였다고 가정해볼까요?

 

 

위 그림에서 R1을 떼버리고

 

a, b를

 

디지털멀티미터로 전압을 측정한 뒤

 

(그값이 뭔지는 몰라도)그 값을 V(th) 라고 가정해보겠습니다.

 

 

이번에는 위 그림에서 선형적인 회로 내부에 있는

 

전원들을 끄고

 

a, b를

 

디지털멀티미터로 저항을 측정한 뒤

 

(그값이 뭔지는 몰라도)그 값을 R(th) 라고 가정해보겠습니다.

 

V(th) = I(th) * R(th)라는 수식이

 

만족한다는 것은 지금까지 회로이론 포스팅을 주의 깊게 보신분이라면

 

누구나 다 알 겁니다.

 

 

 

 

다시 아래 그림을 보겠습니다.,

 

 

R1을 떼버리고

 

a, b 양단을

 

디지털 멀티미터로 전압을 측정했더니

 

V2가 나왔고...

 

V2를 제거한 뒤 a, b 양단을

 

디지털 멀티미터로 저항을 측정했더니

 

저항 R100이 찍혔습니다.

 

이 회로도 뭔지 잘모르지만

 

V2 = I2 * R100 + I2 * R1 이라는 옴의 법칙이 성립하겠죠?

 

자 그럼 정리해봅시다

 

V(th) = I(th)* R(th) + I(th)*R1         --------- 수식 1

V2 = I2*R100 + I2*R1  --------- 수식2

 

위 두 가지 수식에서

 

I(th)가 I(2)와 같고

 

R(th)가 R100이 같다면

 

두 회로는 동일한 회로라고 볼 수 있나요???

 

 

이 말을 바꿔말하면 어떻습니까?

 

우리가 회로를 쉽게 해석하기 위해서

 

 

위와 같은 복잡한 회로(그림1)가 주어졌더라도

 

 

위와 같이(그림2) 간단하게 만든다면

 

회로해석이 더 쉽지 않을까요?

 

그림1의 경우라면 R1이 100OHM에서 200OHM 으로 증가할 경우

 

처음부터 네모박스 부분부터 메시해석, 키르히호프 법칙등...

 

여러 요소들을 다시 회로 해석을 해야하는 반면

 

그림 2의 경우라면 R1이 R2로 바뀌었다 하더라도 크게 무리가 없습니다.

 

한마디로

 

네모박스친 부분이 선형회로이기만 한다면

 

안의 구조는 부하를 해석하는데 있어서 그닥 중요하지 않다 이겁니다.

 

얼마나 대단한가요???!!

 

---

 

제 생각에는 여기까지 말씀드렸다면

 

왜 테브난 등가회로를 사용하는지 어떤식으로 회로에 적용되는지 이해하셨으리라

 

생각합니다.

 

그렇담 어떻게 테브난 등가회로 V(th)를 구하고

 

테브난 등가저항 R(th)를 구할까요?

 

이미 솔루션은 드렸습니다.

 

STEP 1 테브난 등가전압 구하기

 

R1을 떼버린 상태에서 a, b에 디지털 멀티미터를 갖다대 전압값을 측정한다

 

그 값이 V(th)라고 볼 수 있습니다.

 

왜 R1을 떼는가 궁금할 수 있는데

 

우리가 알고 싶은건 R1이 없을때 선형적인 회로가 어떤 OUTPUT을 내고 있는 가를

 

독립적으로 보고 싶은겁니다.

 

R1이 없다 하더라도 고정적인 값(테브난 등가전압)이 뭔지 궁금하고 또 그것을 알기위해

 

이런 수고를 하는 것이니.

 

R1을 떼고서 저항을 측정하는게 맞겠죠.

 

 

STEP 2 테브난 등가저항 구하기

 

등가저항을 구하는 방법은 조금 까다로울 수 있겠네요.

 

먼저, R1을 떼버리고 생각하는 부분은 동일합니다.

 

R1이 영향을 끼지지 않도록 한뒤 나머지가 어떻게 변화하는지를 확인하고 싶은거니까요.

 

헌데... 경우가 2가지로 나뉩니다.

 

선형적인 회로라고 표기되어 있는부분에

 

종속 전원을 가지고 있느냐 아니냐.

 

종속전원을 가지고 있지 않다면

 

단순히 독립전원을 꺼버리고(꺼버린다는 의미는 독립전원을 없애고 단락상태로 만든다는 의미) a, b를 

 

멀티미터로 찍어서 V(th)를 구하면 됩니다.

 

종속전원을 가지고 있는 경우에는

 

종속전원을 제외한 독립전원을 다꺼버린뒤

 

외부에서 전압을 1[V]를 인가하는 방법을 생각 할 수 있는데

 

이게 무슨 의미인지 헷갈릴 수 있어 설명을 추가합니다.

먼저 위와 같은 회로가

 

주어졌다면.

 

R1은 부하측이니 일단 제거합니다.

 

그렇담

 

아래 그림처럼 되겠지요?

 

 

이때 양 개방단자를 멀티미터로 찍는데

 

그전에 V2를 끄고 단락상태로 만든다음

 

마찬가지로 VCVS2도 꺼야 마땅하나

 

문제는 VCVS2가 외부요인에 종속되어 골치가 아픈경우입니다.

 

결과론적으로 보면

 

위 그림같은 경우야 V2에 종속되어 사실상 꺼버려도 무관하겠지만

 

우리는 실제로 선형적인 회로가 어떻게 생겼는지 일일히 관찰하기도 어려울 뿐더러

 

어떤 변수가 서로 얽히고 섥혀있는지 알기도 힘듭니다.

 

해서 편법을 씁니다. 

 

아래 그림에서

V2만 꺼버리고 VCVS2는 냅둔 상태에서

 

외부에서 1[V] 전압원을 인가하는 겁니다.

 

그리고 a 단자쪽으로 들어가는 전류를 I(o)로 두어

 

전류를 구하여

 

1[V] 외부전압원 / I(o) 멀티테스터기 측정전류치 = R(th)

 

라는 수식을 얻어낼 수 있는 것이죠.

 

마지막에 말로풀어 쓰려고 하니 다소 내용이 난잡해집니다.

 

해서 다음편에서는 예제를 간략하게 소개하겠습니다.

 

오늘은 여기까지 마무리할게요.

 

끝.