안녕하세요.
자계미남입니다.
회로이론을 공부하다보면
늘 해왔던 질문들이 있었어요.
아마 여러분들도 마찬가지일 겁니다.
.

.
우리가 대부분 공부하기 힘들었던 이유는
책의 두께가 너무 말도 안되게 두껍고
말은 도무지 이해도 안가는 어려운말을 써놓으니
재미도없고 할양은 많고
공부는 당연히 제대로 되지도 않고
효율도 떨어지기 때문에 시험기간이면
밤새는일이 허다했을테죠.

참...
아직도
회로이론책을 보면
설명하고자 하는 내용들이
생각보다 별거 어려운것도 아닌데
왜 이렇게 어렵게 설명을 해놓았나
참 한스럽습니다.
전기를 공부하고
이쪽 길을 시작한지 약 10년이 되었는데요.
아직도 저는
쉽게 배울 수 있는 방법이 있다면
무조건 쉽게 배우는게 좋다고 생각하는 사람입니다.
때문에
이번 클래스도 여러분들께 제가 대학생때
공부하면서 느꼇던 부분들과
이해가 안갔던 부분들.
별것도 아닌데 어렵게 표현한 내용을
쉽게 표현하고자 노력할겁니다.

쉽게 설명하자면
짧은 이야기들이 다소 루즈하게 늘어질 수 도 있을것 같지만
여러분의 이해를 돕기위해서 최선을 다하겠습니다.
그럼 오늘의 클래스 시작해볼까요
먼저 메시해석은 한 포스팅으로 끝날 것 같지는 않습니다.
생각보다 별거 없지만
쉽게 설명하기 위해서는
다소 클래스를 구분해서 설명할 필요가 있어보입니다.
메시라는 것이 무엇일까요?
다들 예측하셨겠지만
.
.
.

일단 이분은 아닙니다...
(죄송합니다...)
메시라는 건
쉽게 말해서
링 회로안에 <또 다른> 링 회로를
포함하지 않는 녀석을 말합니다.
이게 뭔소리냐구요?
링회로를 회로이론에서는 어렵게
루프라는 표현을 씁니다.
저는 루프라는 표현은 지양하겠습니다.
먼저 원이라는 도형에 대해 특징을 살펴볼 필요가 있겠습니다.
원하면 떠오르는게 뭐가있나요?
저는 반지가 떠오릅니다!

원이라는 도형을 가지고 메시를 설명해보겠습니다.

원 모양이 만들어 지기 위해서는
컴퍼스로 그리듯이
위 그림처럼
시계방향으로 돌아서
처음과 끝이 이어져서 만들어지거나
혹은
반시계 방향으로 돌렸을때
원이 만들어질 수 있겠죠.

갑자기 웬 컴퍼스며 원 얘기냐고요?
원은 사실 회로를 비유해서 표현한 것이거든요.
그렇다면 여러분이 익숙한 다음 도형을 볼까요?

위 그림은
여러분이 익히 회로라고 표현하는 류의 그림입니다.
이 그림도 원과 닮아 있습니다.
직사각형이 어떻게 원이냐고요?
자.
공통점이 있습니다.
시작과 끝이 동일한 지점이 존재한다는 것.
이게 포인트입니다.
원을 예로든 것과 같이
전압원에서 시작해서 전압원으로 끝나는게 보이시죠?
이걸 바로 어려운 용어로 루프라고 표현하는 것이죠,
특히 전기를 공부하다보면 루프라는 말이 참
많이도 튀어나올겁니다.

위 그림을 보세요.
반지가 두 개가 있습니다.
큰 반지안에
작은 반지가 있고
마찬가지로
어느 지점에서는
시작과 끝이 같음을 알 수 있습니다.
문제는,
이 반지의 경우에는
내부에 다른반지를 품고 있다는 겁니다.
즉,
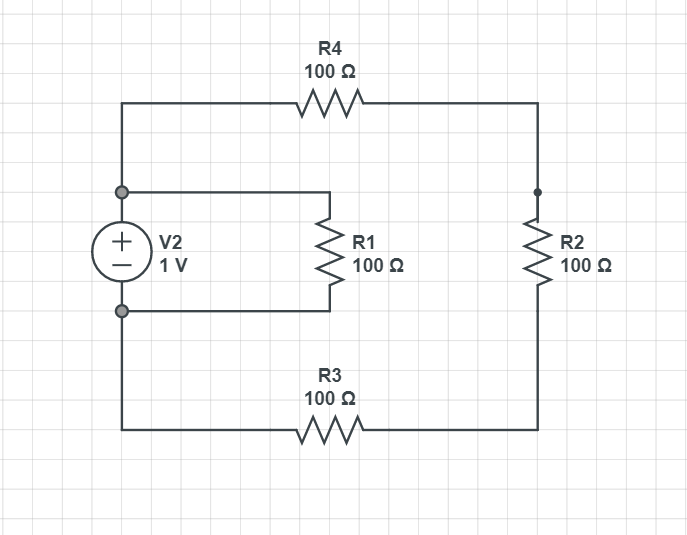
이런 그림과 흡사한데요.
지금 위 회로는
원안에 또다른 원을 품고 있습니다.
여기서.
메시란.
바로
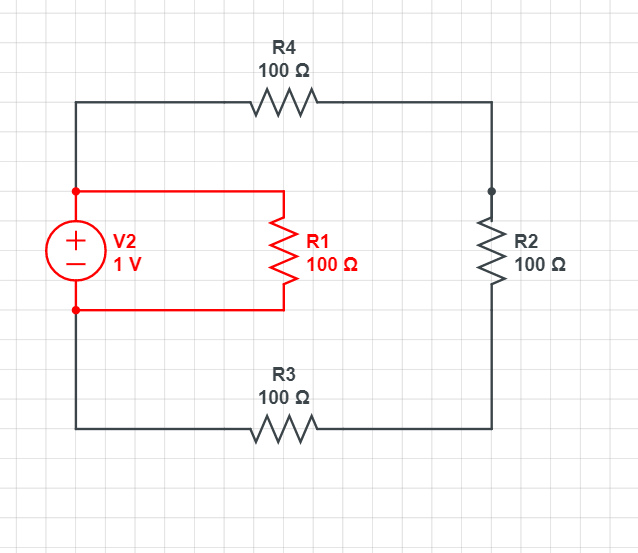
이 부분을 말합니다.
쉽게 표현하면,
원안에 또다른 원을 포함하지 않는 걸 메시라고
표현하는 샘이죠.
그렇다면, 왜
원안에 또다른 원을 포함하지 않는 것을 메시라고 부르며
왜 이게 중요할까요?

우리는 지난시간
노드해석을 공부하면서
여러개의 회로는
사실 개별회로의 집합체라는 사실을 배운바 있습니다.
때문에
아무리 복잡한 회로이더라도
하나의 회로가 여러개 뭉쳐서
나타난 결과물에 불과하기 때문에
결국 소단위 회로로 쪼개서 해석하면 해석하지
못할 것이 없다고 말씀드린바 있습니다.
메시해석도 마찬가지입니다.
다만, 노드해석에서는
미지의 전압을 구하기 위해 키르히호프 전류법칙을 사용했다면
메시해석에서는
미지의 전류를 구하기 위해 키르히호프 전압법칙을 사용한다는
부분이 다르죠.
옴에법칙에 의거
V= I * R
R은 상수이고
전압과 전류는 두 가지 미지수중 한 가지만 표현할 수 있다면
나머지를 구할 수 있죠.
때문에 전압을 변수로 두는 경우와
전류를 변수로 두는 경우를 구분지어
회로를 해석하는 방법이 바로
메시해석과
노드해석인거죠.
메시해석은 노드해석과는 다르게 조금 독특한점이 있습니다.
바로.
평면회로에서만 적용 가능하다는 사실인데요.
평면회로라는 건 말이어렵지
사실은 별거 없습니다.
2차원입니다.
즉, 가로와 세로만 있는 곳에 회로를
겹쳐지는 부분 없이
연필로 그릴 수 있으면 평면회로입니다.
장황하게 말로 풀기보다 쉽게 그림으로 표현하겠습니다.
그림이라 함은, 회로를 실제로 보여드리는게 맞지만
쉽게 설명하고 느낌을 이해하는 것으로 족합니다.
쉽게 배우는게 최고니까요.
아래는 비평면 회로 사례입니다.


다음은 평면 회로의 사례입니다.


이러한 메시해석은
위와같이 평면회로에서만 해석 가능하고
뭔가 교차하는 '가지' 들이 존재하면
해석 불가입니다.
왜 그런지는 다음 클래스를 들어보시면
이해하실 수 있을 것 같네요.
너무 얘기가 길어지면 집중이 떨어지니
다음시간에는 메시해석을
어떻게 하는지 그 방법론에 대해 소개해보겟습니다.
오늘은 여기까지!
끝!
'전기공학 기초이론 > 회로이론' 카테고리의 다른 글
| [회로이론] - 선형 비선형 어디서 많이 들어보긴 했는데 잘모르겠다면???.. (0) | 2021.07.05 |
|---|---|
| [회로이론] - 메시해석? 어떻게 하는건데? [2탄] (1) | 2021.06.20 |
| [회로이론] - 누가 이런식으로 전기를 알려줘? (노드해석 전압원이 있을때 문제) (1) | 2021.06.02 |
| [회로이론] - 전압원이 있을때 노드해석은 어떻게 하는거지? (1) | 2021.05.25 |
| [회로이론] - 회로 해석에 필요한 중요 요소 노드 . 그래서 노드가 뭔데? (0) | 2021.04.21 |



