'회로이론시험'에 해당되는 글 2건

안녕하세요

 

오늘의 포스팅은 되도록

 

짧게 끝내도록 하죠

 

그럼...

 

 

지난시간에 이어서 바로 직진해볼게요.

 

한 사례를 들어볼게요.

 

 

지난시간에 링을 설명하면서

 

메시가 무엇인지 설명했었죠

 

메시가 기억안나시는 분은 다시 복습하고 오시길 추천드립니다.

 

지난시간 내용을 다 안다는 전제하에 문제를 풀어보죠.

 

먼저 메시해석을 하기위해선 무엇을 해야할까요?

 

1. 여러개의 메시에서 메시 전류를 i1, i2, i3, i4...... 할당한다.

 

2. n개의 메시의 각각에 키르히호프전압법칙을 적용해본다.

[이때 옴의 법칙을 적절히 이용한다.]

 

3. 메시 전류들을 구하기 위해 n개의 연립방정식을 푼다.

 

위 3과정이

 

메시해석의 전부입니다.

 

너무나 간단하죠.

 

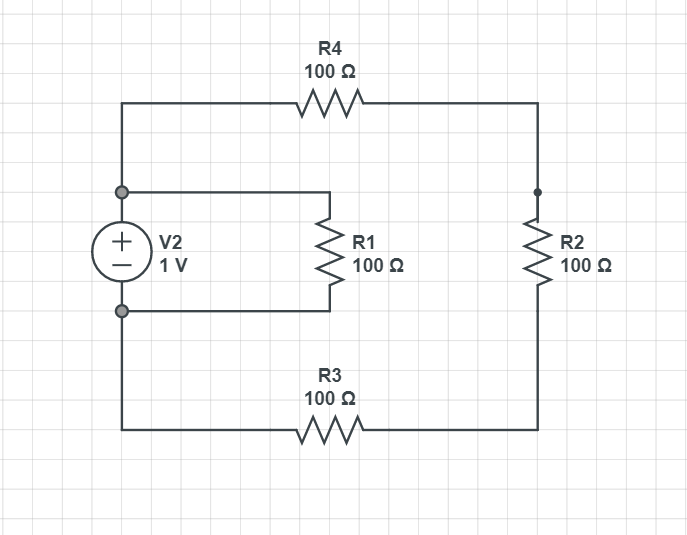
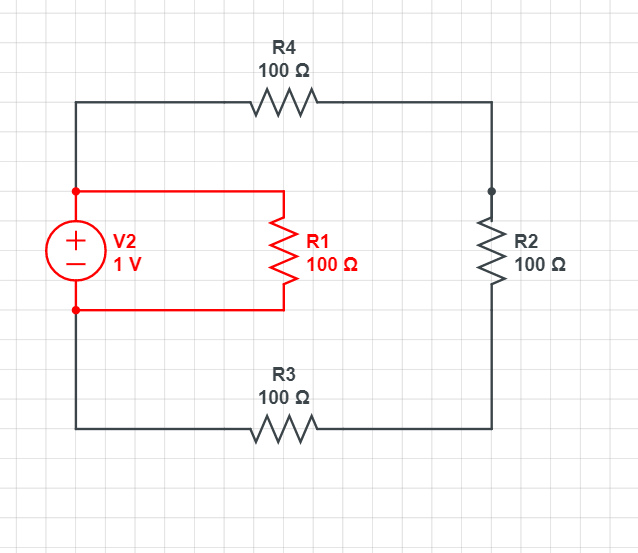
위 예시에는 2개의 메시가 있어요.

 

1번 메시는.

 

 

이렇게 생겼죠?

 

문제를 푸는거야... 너무쉽습니다.

 

-V2 + 100 * i1 + 100 * ( i1 + i2) =0

 

다음은.

 

2번 메시입니다.

 

 

이 수식도 위와 마찬가지 방법으로 구할 수 있겠죠.

 

다만 전류의 방향이 반시계 방향인 것은.

 

V3 전압원의 극방향이

 

V1과 다르기 때문입니다.

 

사실 메시 해석에 있어서는 전류의 방향을 모른다고 가정하고

 

임의의 방향으로 잡아도 상관없습니다.

 

어차피 계산결과 음의 부호가 나오면

 

내가 구한 전류방향의 반대방향으로 흐르는구나.

 

알 수 있거든요.

 

어쨋든.

 

수식을보면 아래와 같습니다.

 

-V3 + 100 * i2 + 100 * (i1+ i2) =0

 

자 그럼.

 

두 수식을 연립해봅시다.

 

100 * i1 + 100 * ( i1 + i2) = V2

100 * i2 + 100 * ( i1+ i2 ) = V3

 

V2와 V3의 값은 정해져있는 상수값이며

 

변수는 i1과 i2이니 두개의 미지수는

 

두개의 방정식으로 답을 찾을 수 있다는 결론이 나타납니다.

 

답은 여러분이 찾아보세요.

 

자 그럼 아래와 같은 경우는 어떻게 메시해석을 할까요?

 

 

 

포인트는 전류원인데요

 

 

 

대체 중첩되는 요부분을 어떻게 해석해야겠냐는 겁니다.

 

R3에 흐르는 전류가 얼마일까요?

 

너무 쉽죠.

 

당연히 1[A] 일겁니다

 

직렬로 연결되있으니까요 

 

문제는 R3를 건너

 

R1과 R2 둘의 메시전류로 쪼개질때 어떻게 쪼개질 것이냐가 문젠데.

 

이를 위해서 우리는 일반적인 방법으로 연립방정식을 세우려 할겁니다.

 

뭐 이런식이죠.

 

전체 회로가 이렇게 생겼다면.

 

 

여기서 한번 메시를 돌리고

 

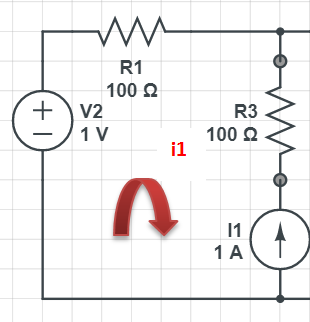
KVL 적용하면

 

-1 * i1 * R1 - 100 = 0

 

i1 = 1.01 [A]

 

가 바로 나왔습니다.

 

이게 맞을까요?

 

Nope

 

이렇게 푸신 여러분은

 

재수강입니다.

 

-

왜냐고요?

 

키르히호프 전압법칙은

 

폐경로에서만 먹힌다는 기초를 잊었기 때문이죠.

 

회로를 다시봅시다.

 

우리가 회로이론에서 다루는건 이상적인 회로에 대해서 다룬다고

 

이전에 설명드린바 있었죠.

 

이상적인 전류원은

 

이상적인 소자로

 

자체 소모 전압이 0이며

 

저항이 무지막지하게 크다는거

 

설명드린바 있습니다

 

V = I * R 이라는 옴의법칙에서

 

보아도 알 수 있습니다.

 

 V = 0 이고,

 

I는 0이 아닌 상수값이니

 

R은 적어도 무한대가 되어야 이 수식이

 

성립할 가능성이 있겠죠.

 

저항이 무한대라는 것은 무엇을 의미할까요?

 

네.

 

그렇죠.

 

개방회로입니다.

 

전류원이 떡하니 센터에 포진되어 있는 경우 

 

메시해석 시에는

 

걍 씹어주시면 되겠습니다.

 

개방회로니까요

 

따지고보면

 

위회로는 키르히호프 전압의 법칙을 적용하려는 관점으로

 

동일한 회로를 그렸을때 아래와 같이 표현될겁니다.

 

요렇게 회로를 해석하면 되겟지요.

 

허나.

 

두개의 작은 메시가 개방회로로 인해서

 

하나의 메시를 이루었다해서

 

메시전류가 동일한건 아니랍니다.

 

때문에.

 

키르히호프 전압법칙을 사용할때

 

-V1 + i1*100 -i2 * 100 + V3 = 0

 

이 되어야 

 

맞는 수식이 되겠지요.'

 

그럼 우리는 또다른 수식을 찾아야만하는데

 

과연 어떤수식을 또 찾아낼 수 있을까요?

 

여기서 여러분이 헷갈릴만한 사실 하나를 던져보려 합니다.

 

아까 분명 이회로는 개방되어 있다 했었죠.

 

이 회로.

 

개방되어 있지만.

 

전류는 흐릅니다

 

어떻게 그럴수 있냐고요?

 

네 가능합니다.

 

이세상에 없는 전기거든요.

 

어쨋든 키르히호프 전압법칙으로부터

 

첫 번째 미지수 수식을 알아냈다면

 

이제는 키르히호프 전류법칙으로 부터

 

아래 수식을 하나 더 알아낼 수 있습니다.

 

바로 요부분 인데요.

 

-i1 - i2 = 1[A]

 

이 될겁니다.

 

-V1 + i1*100 -i2 * 100 + V3 = 0

 

-i1 - i2 = 1[A]

 

 

100 * i1 =100 * i2

 

i1 = i2

 

i1= 0.5[A]

 

i2 = 0.5[A]

 

매번 공부하면서 느끼는 거지만,

 

기초가 왜중요한지

 

왜 우리는 늘 기초를 망각하고 어려워하는지 뼈저리게 느끼곤합니다.

 

현업에 뛰는 저로써도 기초는 어렵고요.

 

혹시나 계산이나 수식에 문제가 있다면 피드백주세요.

 

오늘은 여기까지입니다.

 

고맙습니다. ㅎ

 

 

안녕하세요.

 

자계미남입니다.

 

회로이론을 공부하다보면

 

늘 해왔던 질문들이 있었어요.

 

아마 여러분들도 마찬가지일 겁니다.

 

.

.

우리가 대부분 공부하기 힘들었던 이유는

 

책의 두께가 너무 말도 안되게 두껍고

 

말은 도무지 이해도 안가는 어려운말을 써놓으니

 

재미도없고 할양은 많고

 

공부는 당연히 제대로 되지도 않고

 

효율도 떨어지기 때문에 시험기간이면

 

밤새는일이 허다했을테죠.

 

 

참...

 

아직도

 

회로이론책을 보면

 

설명하고자 하는 내용들이

 

생각보다 별거 어려운것도 아닌데

 

왜 이렇게 어렵게 설명을 해놓았나

 

참 한스럽습니다.

 

전기를 공부하고

 

이쪽 길을 시작한지 약 10년이 되었는데요.

 

아직도 저는

 

쉽게 배울 수 있는 방법이 있다면

 

무조건 쉽게 배우는게 좋다고 생각하는 사람입니다.

 

때문에

 

이번 클래스도 여러분들께 제가 대학생때

 

공부하면서 느꼇던 부분들과

 

이해가 안갔던 부분들.

 

별것도 아닌데 어렵게 표현한 내용을

 

쉽게 표현하고자 노력할겁니다.

 

 

쉽게 설명하자면

 

짧은 이야기들이 다소 루즈하게 늘어질 수 도 있을것 같지만

 

여러분의 이해를 돕기위해서 최선을 다하겠습니다.

 

그럼 오늘의 클래스 시작해볼까요

 

---

 

먼저 메시해석은 한 포스팅으로 끝날 것 같지는 않습니다.

 

생각보다 별거 없지만

 

쉽게 설명하기 위해서는

 

다소 클래스를 구분해서 설명할 필요가 있어보입니다.

 

메시라는 것이 무엇일까요?

 

다들 예측하셨겠지만

 

.

.

.

 

 

 

일단 이분은 아닙니다...

 

(죄송합니다...)

 

 

 

메시라는 건

 

쉽게 말해서

 

 링 회로안에 <또 다른> 링 회로를

 

포함하지 않는 녀석을 말합니다.

 

이게 뭔소리냐구요?

 

링회로를 회로이론에서는 어렵게

 

루프라는 표현을 씁니다.

 

저는 루프라는 표현은 지양하겠습니다.

 

먼저 원이라는 도형에 대해 특징을 살펴볼 필요가 있겠습니다.

 

원하면 떠오르는게 뭐가있나요?

 

저는 반지가 떠오릅니다!

 

 

 

원이라는 도형을 가지고 메시를 설명해보겠습니다.

 

 

 

원 모양이 만들어 지기 위해서는

 

컴퍼스로 그리듯이

 

위 그림처럼

 

시계방향으로 돌아서

 

처음과 끝이 이어져서 만들어지거나

 

혹은

 

반시계 방향으로 돌렸을때

 

원이 만들어질 수 있겠죠.

 

갑자기 웬 컴퍼스며 원 얘기냐고요?

 

원은 사실 회로를 비유해서 표현한 것이거든요.

 

그렇다면 여러분이 익숙한 다음 도형을 볼까요?

 

 

 

위 그림은

 

여러분이 익히 회로라고 표현하는 류의 그림입니다.

 

이 그림도 원과 닮아 있습니다.

 

직사각형이 어떻게 원이냐고요?

 

자.

 

공통점이 있습니다.

 

시작과 끝이 동일한 지점이 존재한다는 것.

 

이게 포인트입니다.

 

원을 예로든 것과 같이

 

전압원에서 시작해서 전압원으로 끝나는게 보이시죠?

 

이걸 바로 어려운 용어로 루프라고 표현하는 것이죠,

 

 

특히 전기를 공부하다보면 루프라는 말이 참

 

많이도 튀어나올겁니다.

위 그림을 보세요.

 

반지가 두 개가 있습니다.

 

큰 반지안에

 

작은 반지가 있고

 

마찬가지로

 

어느 지점에서는

 

시작과 끝이 같음을 알 수 있습니다.

 

문제는,

 

이 반지의 경우에는

 

내부에 다른반지를 품고 있다는 겁니다.

 

즉,

 

 

이런 그림과 흡사한데요.

 

지금 위 회로는 

 

원안에 또다른 원을 품고 있습니다.

 

여기서.

 

메시란.

 

바로

 

 

이 부분을 말합니다.

 

쉽게 표현하면,

 

원안에 또다른 원을 포함하지 않는 걸 메시라고

 

표현하는 샘이죠.

 

그렇다면, 왜

 

원안에 또다른 원을 포함하지 않는 것을 메시라고 부르며

 

왜 이게 중요할까요?

 

 

우리는 지난시간

 

노드해석을 공부하면서

 

여러개의 회로는

 

사실 개별회로의 집합체라는 사실을 배운바 있습니다.

 

때문에

 

아무리 복잡한 회로이더라도

 

하나의 회로가 여러개 뭉쳐서

 

나타난 결과물에 불과하기 때문에

 

결국 소단위 회로로 쪼개서 해석하면 해석하지

 

못할 것이 없다고 말씀드린바 있습니다.

 

메시해석도 마찬가지입니다.

 

다만, 노드해석에서는

 

미지의 전압을 구하기 위해 키르히호프 전류법칙을 사용했다면

 

메시해석에서는

 

미지의 전류를 구하기 위해 키르히호프 전압법칙을 사용한다는

 

부분이 다르죠.

 

옴에법칙에 의거

 

V= I * R

 

R은 상수이고

 

전압과 전류는 두 가지 미지수중 한 가지만 표현할 수 있다면

 

나머지를 구할 수 있죠.

 

때문에 전압을 변수로 두는 경우와

 

전류를 변수로 두는 경우를 구분지어

 

회로를 해석하는 방법이 바로

 

메시해석과

 

노드해석인거죠.

 

메시해석은 노드해석과는 다르게 조금 독특한점이 있습니다.

 

바로.

 

평면회로에서만 적용 가능하다는 사실인데요.

 

평면회로라는 건 말이어렵지

 

사실은 별거 없습니다.

 

2차원입니다.

 

즉, 가로와 세로만 있는 곳에 회로를

 

겹쳐지는 부분 없이

 

연필로 그릴 수 있으면 평면회로입니다.

 

장황하게 말로 풀기보다 쉽게 그림으로 표현하겠습니다.

 

그림이라 함은, 회로를 실제로 보여드리는게 맞지만

 

쉽게 설명하고 느낌을 이해하는 것으로 족합니다.

 

쉽게 배우는게 최고니까요.

 

아래는 비평면 회로 사례입니다.

 

다음은 평면 회로의 사례입니다.

 

 

이러한 메시해석은

 

위와같이 평면회로에서만 해석 가능하고

 

뭔가 교차하는 '가지' 들이 존재하면

 

해석 불가입니다.

 

왜 그런지는 다음 클래스를 들어보시면

 

이해하실 수 있을 것 같네요.

 

너무 얘기가 길어지면 집중이 떨어지니

 

다음시간에는 메시해석을

 

어떻게 하는지 그 방법론에 대해 소개해보겟습니다.

 

오늘은 여기까지!

 

끝!