'전기공학 기초이론'에 해당되는 글 57건

어느덧 회로이론 포스팅이 전체의 중간정도를 지나가는것 같네요.

사실 예전에 학교 다니면서 열심히 공부했을 때에는 이맘쯤 해서  중간고사를 치렀던 것 같습니다.

오늘 배워볼 것은

커패시터입니다.

캐패시터라고 부르기도 하고

콘덴서라고 부르기도 합니다.

다 동일한 이름을 다르게 표현한 것이니 모두 같은 의미로 생각하시면 되겠습니다.

자.

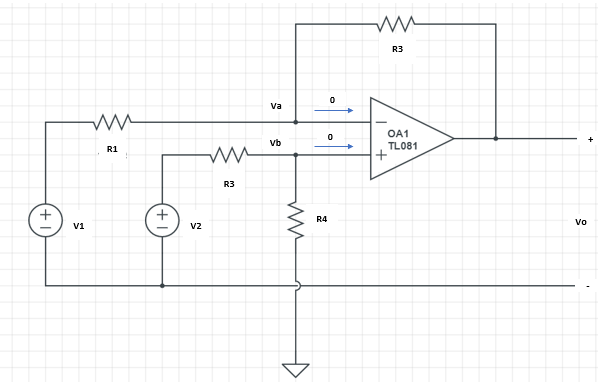
우리는 지금껏 저항과 전압원 전류원으로만 이루어진 소자를 바탕으로 회로를 구성했었습니다.

아래처럼요.

저항은 전류의 흐름을 방해하는 소자로서

발열이 발생함으로써 전기에너지를 빛이나 열에너지로 변환해준다면

우리가 오늘 배울 커패시터는, 전기에너지 자체를 보관하는 느낌으로 접근하시는게 좋겠습니다.

자.

그럼 어떻게 전기에너지를 저장할 수 있느냐?

그림을 보시면 전압원 V1에서

양전하가

하나의 극판에 모이고

음전하가

나머지 하나의 극판에 모이게 되는 모습을 발견할 수 있을겁니다.

상식적으로 이런상황이라고 하면

+ 와 -가 붙으려는 성질때문에

자석과 같은 인력이 작용하여

두극판이 붙어버리겠죠.

물론 저항이 아주 작다면 터져버릴 수 도 있죠.

허나 물리적인 어떤 에너지에 의해,

혹은 절대 닿을 수 없는 두 극판을 기구적, 화학적, 전기적으로 설계하였다면

어떻겠습니까?

+와 -는 끌어당기려는 성질 때문에

마치 양극판에 +와 -가 똘똘 뭉쳐있는 모습으로 남아있을겁니다.

마치 배터리처럼요.

이를 실제 회로도로 표현하면 아래와 같습니다.

C2라고 표현된 짝대기 두개가

바로 커패시터를 말하는 것이며,

단위는

패럿(FARROT)이라는 단위를 사용합니다.

저항의 (OHM)과 같은 개념이죠.

두 극판사이에는 공기나, 세라믹, 종이, 운모와 같은 절연체를 사용하게 되고

양극판은 알루미늄을 주로 사용합니다.

이러한 커패시터는 전하를 한곳으로 응축시켜주는 역할을 하기에

마치 건전지와 비슷하죠.

건전지 역시 +극과 -극이 존재하고

평소에는 절연되어 있다가

어떠한 부하를 연결하여 회로가 개통될때

전기가 흐르게 되죠.

아래처럼요.

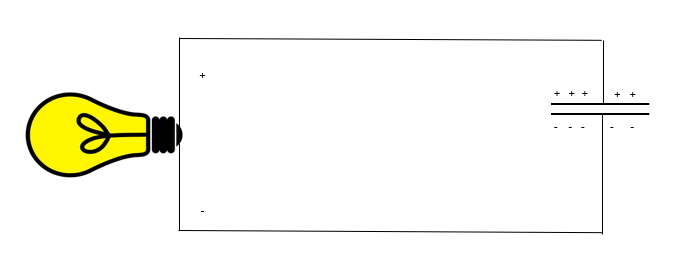
물론 이러한 커패시터는 실제로 건전지와 같이 쓰일 수는 없습니다.

건전지는 방전이 아주 천천히 이루어지는 반면

커패시터의 방전은 엄청나게 빠른시간에 일어납니다.

무슨소리인가 하면.

커패시터가 그림1처럼

한극판에 +가 모여있고

나머지 한 극판에 -가 모여있는 상태를

충전상태라고 표현하면

그림2처럼

커패시터 양단에 어떠한 부하를 투입했을때

전하가 이동하는 것을 방전된다 라고 표현하는데

건전지는 화학작용을 통해서 방전이 천천히 일어나므로

유의미한 방법으로 전구를 켤 수 있는데

*유의미하다는 것은 전기의 움직임을 사람이 원하는 용도대로 사용할 수 있다는 의미입니다.

*전구는 오랜시간 지속되서 켜지는게 좋겠죠.

커패시터는 특성마다 다르겠지만 1초도 안되는 짧은 시간에 방전이 이루어집니다.

해서. 커패시터를 우리가 생각하는 건전지 개념으로 이해하는 것은 좋으나

건전지와 똑같은 기능을 수행할 수 있다고 이해하시면 안되겠습니다.

이러한 커패시터는 특별한 관계가 성립하는데요

Q = C * V

Q = 전하량

C = 비례상수

V = 전압

전하량이 전압과 비례관계라는거죠.

이 이야기는 다음시간에 이어서 자세히 풀어보도록 할게요.

지난 시간에는 연산증폭기 중

가산증폭기를 공부했었습니다.

차분증폭기는 가산증폭기와 원리가 비슷합니다.

해서 짧게 이번시간 마무리 해보도록 하겠습니다.

가산증폭기가

여러 입력이 존재하는 경우 입력에 가중치를 두어 합산한 값을 출력하는 것이라면

차분증폭기는

두 입력 사이의 차이만큼 증폭하는 기기입니다.

두입력의 차이만큼 증폭한다는 의미는 돌려 표현하면

두입력상 공통적으로 인입되는 신호는 무시하겠다는 의미로 해석하시면 되는데요.

그림을 보겠습니다.

차분증폭기는 이렇게 생겼습니다.

외부에 전압원 두개가 있고

이상적인 연산증폭기를 가정하고 문제를 해석하는 것이기 때문에

양 입력단 전류는 0입니다.

(V1 - Vo) / R1 = (Va - Vo) / R2

라고 쓸수 있겠죠.

또한

(V2 - Vb)/R3 = Vb / R4 입니다.

Va = Vb

이 수식을 잘 정리하면

아래 수식을 얻을 수 있어요.

Vo = {R2(1+R1/R2)}*V2/{R1(1+R3/R4)} - V1* R2/R1

우리가 위 수식에서 알 수 있는 건.

V1 = V2 가 동일하고

R1/R2 = R3/R4

비율이 성립될 때

아래 수식으로 정리될 수 있다는 사실인데

Vo = (R2/R1)*(V2-V1)

정리해보면 V2와 V1의 차이만큼을 R2와 R1의 비율로 출력을 조정할 수 있다 입니다.

예를들어 이런겁니다.

V2 = 6[V]

V1 = 5[V]

R1 = R2

인 경우에는

단순히 뺄셈 계산기의 역할을 수행할겁니다.

허나

V2 = 6[V]

V1 = 5[V]

R2/R1= 0.8 인 경우에는

0.8[V] 출력이 나옵니다.

뺄셈 계산기는 뺄셈 계산긴데

감도를 조정할 수 있다는 겁니다.

어디에 이런게 응용될 수 있을까요??

R2/R1이 가변저항으로써 그 비율이 계속 변할 수 있다고 한다면,

어떤 전압을 넣던

일정한 출력을 내고 싶은 경우가 있어요.

예시에 든것처럼 0.8[V]가 나오게끔 하고싶은데

어떤 이유로

V2가 7[V]

V1이 5[V]

들어갔다면 어떨까요?

R2/R1 비율이 0.8로 동일하다고 했을때

출력은 1.6[V]가 나올겁니다.

허나 R2/R1의 비율이 0.4가 된다면요?

출력은 0.8[V]가 나오겠죠?

즉 입력의 값자체가 통제가 안되고 변하더라도

저항의 비율을 통해서

일정한 출력을 내보낼 수 있다는 의미...!

정전압 소자가 구현되었네요.

지난시간과 다르게 내용 설명이 다소 짧았습니다.

가산기와 감산기는 그 맥락이 같기 때문에

자세한 설명보다는 이상적인 연산증폭기가 이런 원리로 응용되고 있다는 사실을

숙지하실 수 있도록 이글을 작성했습니다.

이로써 이상적인 OP AMP 포스팅을 마치겠습니다.

이 포스팅을 시작하기에 앞서

어떠한 방법으로 이산적인 연산증폭기가

계산에 응용될 수 있는지 말씀드렸었죠.

미분 적분과 같은 고급계산에 대해서 설명하지는 못했지만,

모든 연산수식이 덧셈과 뺄셈에서 이루어지는 것이니 만큼

기초적인 원리를 탄탄히 이해하시고 필드엔지니어로 몸담으신다면

분명 배웠던 것들이 서로 매칭되는 때가 있을겁니다.

지난시간에

반전증폭기에 대해서 공부했었습니다.

사실 비반전 증폭기도 있지만

내용이 매우 흡사하여 생략하고

다음 포스팅으로 넘어가보도록 하겠습니다.

오늘 배울 것은 가산증폭기 입니다.

OP AMP를 처음 포스팅할때 분명히 말씀드렸죠.

OP AMP가 어떻게 덧셈과 뺄셈 계산이 가능한건지

이런 원리가 무엇인지에 대해서요.

띄엄 띄엄 포스팅하여 다소 흐름이 끊긴 느낌이 있지만

포스팅을 꾸준히, 정독하신 분이시라면 얼추 개념이 잡혔으리라 확신합니다.

오늘은 더하기 기능을 수행하는 OP AMP의

가산증폭기를 본격적으로 알아보도록 하겠습니다.

가산 증폭기는 입력이 여러개 존재할 때

가중치를 주어

더해진 값을 출력으로 내보내는 장치입니다.

가중친 뭐고 대체 어떻게 준다는걸까요??

먼저 아래 그림을 봅시다.

가산증폭기를 표현한 그림에서

R1에 흐르는 전류를 i1

R2에 흐르는 전류를 i2

R3에 흐르는 전류를 i3

이라고 가정하고

OP AMP의 양 입력단자(OP AMP 상 -와 + 입력부분) 전위를

Va라고 표현하겠습니다.

키르히호프 전류 법칙에 의하여

i1+i2+i3 = I1

된다는 사실은 인지상정이죠.

옴의법칙에 의하여 위 수식을

아래처럼 정리할 수 있습니다

i1 = (v1 - Va) / R1

i2 = (v2 - Va) / R2

i3 = (v3 - Va) / R3

여기서 주목해야할 부분은 저항 R4에 흐르는 전류도

I1 이라는점.

이상적인 OP AMP를 가정하고 문제를 풀기때문에 그렇습니다.

이마저도 무슨말인지 이해가 안가신다면 복습이 안된 것이니

차근차근 앞 포스팅으로 넘어가서 정독해주세요.

I1은 이렇게도 표현할 수 있습니다.

I1 = { Va - V(out) } / R4

연두색 음영에 기술된 모든식을 종합하여 정리해보면

아래 수식이 성립하겠죠.

(v1 - Va) / R1 + (v2 - Va) / R2 + (v3 - Va) / R3 = { Va - V(out) } / R4

여기서 다시 중요한 부분!

이상적인 OP AMP를 가정하였기 때문에

Va는 0이 된다는점.

(모르겠다면 앞에 내용을 다시 복습하고 오세요!)

때문에 수식은 이렇게 최종 정리됩니다.

v1 / R1 + v2 / R2 + v3 / R3 = - V(out) / R4

수식은 여기까지 증명되었죠.

근데 이 수식이 대체 무엇을 의미하냐는 거가 중요하겠죠.

수식을 가만히 들여다보니

V(out)은 출력 전압인데.

저항의 비율을 통해서 입력 전압을 조정할 수 있고

전압을 펌핑할 수 있다 정도로 이해할 수 있겠죠?

예를 들어 이겁니다.

v1 = 1[V]

v2 = 2[V]

v3 = 3[V]

이고,

R1, R2, R3, R4가 모두 1[ohm] 으로 동일하다고 하다면

V(out) = -6[V]가 될 겁니다.

결국  R1, R2, R3, R4가 모두 1ohm 이라면

내가 수학적으로 계산할 수 있는 수식은 (1 + 2 + 3)*(-1)

딱 한가지인 겁니다.

하지만.!

저항을 적절히 섞는다면 입력전압의 비율을 조정할 수 있고

결국 출력전압이 영향을 받는다는게 이 수식의 키포인트입니다.

즉,  입력전압은 정해진 값(1[V], 2[V], 3[V])이 들어가더라도

저항의 비율로 입력 값을 조정할 수 있기에

다양한 덧셈식을 표현하는게 가능해집니다.

물론.

입력전압 자체를 바꾸면 되는거 아니냐고 반문하실 수 있는데,

전압을 바꿔주는 장치보다.

저항이 훨씬 쌉니다.

단순한 계산 기능이 필요한 것이며

정밀하지 않아도 된다면,

저라면

엔지니어 관점에서 저항을 쓰겠습니다.

오늘은 여기까지 하겠습니다.

안녕하세요.

오랜만에 다시 회로이론 포스팅이네요.

회로이론 포스팅하다가 왜 뜬금없이 반도체 분야를 포스팅했었는지

궁금하셨을수도 있으리라 보는데...

어느날 블로그를 들어와보니 포스팅하겠다고 메뉴는 여러개 만들어 놨었는데

막상 대부분의 메뉴 포스팅이 0이고...

회로이론이랑 PLC만 여럿 있더라고요...

해서 이제는 회로이론뿐만 아니라 중간중간 다른 분야 역시 포스팅을

골고루 해볼까합니다. 

시간이 꽤흘렀지만.

우리는 지난시간에 이상적인 OP AMP에 대해서 공부했었습니다.

이상적이라는 말 자체가

이세상에 없는 소자이지만

이것을 배워야 하는 이유는 분명히 말씀드렸었죠.

이상적인 회로 자체가 소자를 만드는데 목표가 될 수 있기 때문이죠.

아무리 이상적인 회로를 만들기 위해 노력해봤자

이상적인 회로를 만들어낼 순 없을겁니다.

하지만 우린 이걸 만들어내기 위해 노력해야 하는겁니다.

서두가 길었습니다.

오늘은 반전 증폭기에 대해서 배워보겠습니다.

반전증폭기는

이렇게 생겼습니다.

특징이 있다고 하면.

전압원 V2중 '+' 극성을

OP AMP의 - 에 입력시켜주고

접지선을 

OP AMP의 +에 입력시켜줌으로써

실제 출력되는 전압을 역으로 이용하는 결과를 빚습니다

반전 증폭기는 논리회로에서 NOT의 신호를 표현하는 것으로.

1 * (-1) = -1

위 수식에서

(-1)의 역할을 OP AMP가 한다고 보시면 되겠네요.

다시 다른 수식을 보면.

1* (-2.5) =  -2.5

위 수식에서

-2.5가 OP AMP 역할을 하는거니까.

여기서 입력과 출력 전압의 비율이 -2.5인 OP AMP라고 볼 수 있고

Vo/Vi = -2.5라고 볼수도 있겠죠.

OP AMP는 실제의 모습으로 보면

어떤 전압이 들어가면

어떤 출력이 나오는 형식입니다.

회로가 복잡하고 어려워보이지만

사실 반전증폭기의 역할의 주내용은 이게 

끝입니다.

어렵게 수식 계산에 주목하지마세요.

수식 계산이 중요한게 아니라

이게(반전증폭기) 뭐할때쓰는건지 원리를 이해하는게 훨씬 이득입니다.

말씀드렸다시피

연산증폭기는 연산기능을 수행하도록 설계되었습니다.

이쯤 설명했으면 연산기능이 어떠한 원리로 수행되는지

이해하셨으리라 생각합니다.

주내용을 이해하셨으니

부수적으로

수식 계산 역시 진행해보겠습니다.

다시 회로를 들고왔습니다.

이상적인 연산증폭기이니 우리는 아래 사실을 정리할 수 있습니다.

일단

I1 = I2

입니다.

I1 = I2를 옴의법칙으로 정리를 적절히 해보면

(V2 - V1) / R1 = (V1 - Vo) / R2

라는것도 쉽게 이해되시죠?

여기에다가 OP AMP의 단자중 '+'가 접지에 연결되어있으므로

V1이 0[V]가 됩니다.

그말은

V2 / R1 = - Vo / R2

라는 이야기인데

V2라는게 입력 전압 Vi와 같으므로

정리하면

Vi / R1 = - Vo / R2

가되죠.

입력과 출력전압을 정리하면

Vo = -Vi * (R2 / R1)

이라는 의미와 일맥상통하며

Vo / Vi = -(R2 / R1)이므로

여기서 나타낸 -(R2/ R1)이

위에서 열심히 설명한 내용중

아래 인용구

"

1* (-2.5) =  -2.5

위 수식에서

-2.5가 OP AMP 역할을 하는거니까.

"

-2.5를 뜻합니다.

이정도면 이해 못하는게 더힘들거에요.

오늘은 여기까지 하겠습니다.