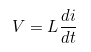'전기공학 기초이론'에 해당되는 글 57건

중간고사 이후의 포스팅

그러니까. 횟수로치면 지지난번 포스팅 이후

약간의 공학 수학 관련 수식이 들어가서 헷갈리거나 어려우실 수 있으실테죠.

아무래도 전기라는 학문이 자연현상을 활용하여

경제적인 효과를 누리고자 하는 학문이다보니

약간의 수식들이 사용되는 경우가 많습니다.

저는 사실 수학을 잘하진 않아서 수학을 폭넓게 이해하고 있진 않습니다만,

대학을 나온 분이라면 대부분 배우는 기초지식(공학수학 정도)

까지는 공부를 해두시는 편이 좋겠습니다.

만약 나는 대학을 안나왔으면 어떻게 해야하나?

그런 분들은

전기라는 포괄적인 개념을 이해하면 됩니다.

제가 포스팅에 대해서 수식에 대해 최소한으로 다루는 이유가 있습니다.

실무에서 엔지니어로 뛰는 경우

실질적인 수식은 컴퓨터가 알아서 다해줍니다.

나는 전체적인 개요를 바탕으로 소프트웨어를 적절하게 구사하면 되고,

스스로 욕심이 있어서 더 깊게 알고싶다 하시면 공부하시면 됩니다.

쉽게말해 수식적인 이해도 중요하지만

보다 중요한건 전기라는 자연현상이 어떻게 생겨먹었는지

그전 체적인 모습을 기억하는게 더중요하단 겁니다.

내몸의 세포가 어떻게 이루어져있는지

DNA구조(수식에 대한 이해)까지는 알지못하지만

사람은 사람을 서로 알아볼 때 아주 세세한 DNA따위 몰라도.

서로를 이해하는데 전혀 문제가 없습니다.

심지어 남녀관계 처럼 복잡한 여러 호르몬의 상호작용이 존재하는 고도의 사고 및 심리현상에도

우리는 그 원인을 분석하지 않습니다. 있는 그대로를 받아들일 뿐이죠.

우리는 아무것도 모르지만 fall in love 하죠.

비유가 적절한진 모르겠으나.

전기도 그렇습니다.

실무를 뛰기 위해서 그정도만 알면됩니다.

내가 연구개발하는 사람이 아니라면요.

서두가 길었습니다.

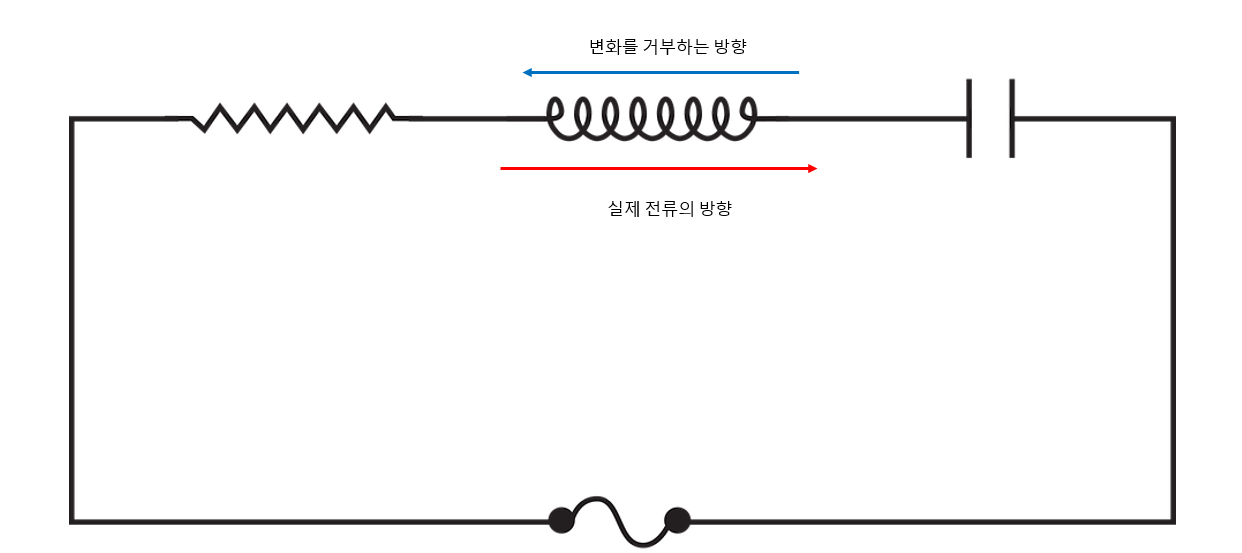
오늘은 무전원 RL 회로를 알아보겠습니다.

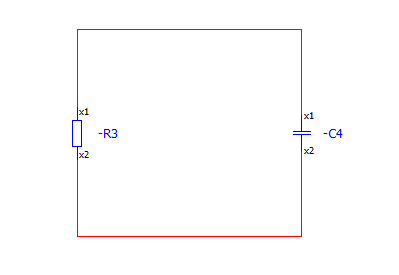
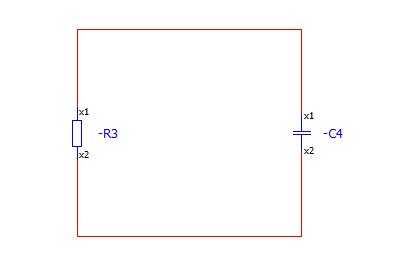
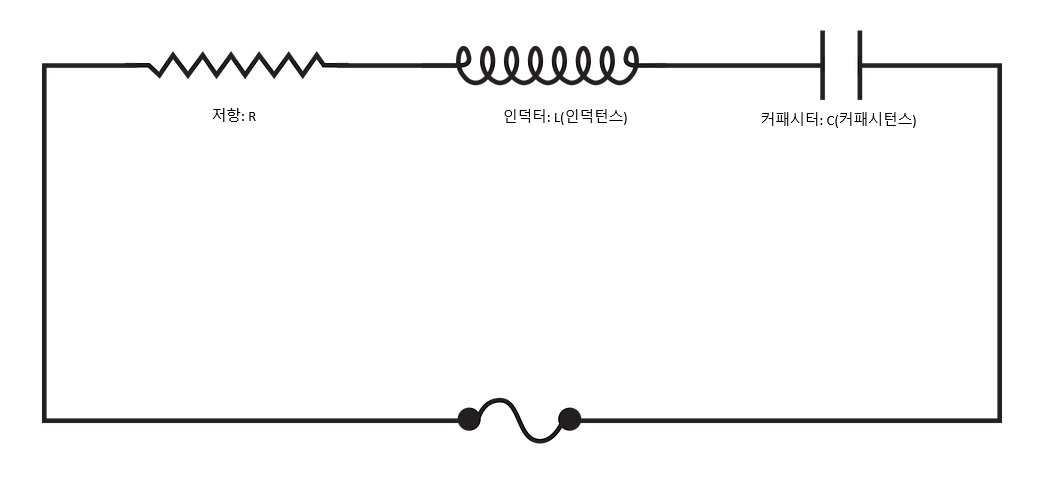
우선, 무전원 RL 회로는 이렇게 생겼습니다.

무전원 RL회로 역시도.

이자체의 회로로는 의미가 없습니다.

전위가 없으니 말이죠.

하지만 어떠한 이유에서건

전기가 흐르다가 어떤 연유에서건 갑자기 끊어진 직후의

상황을 생각해보자는 겁니다.

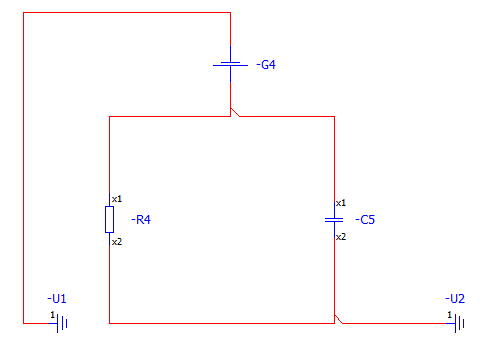
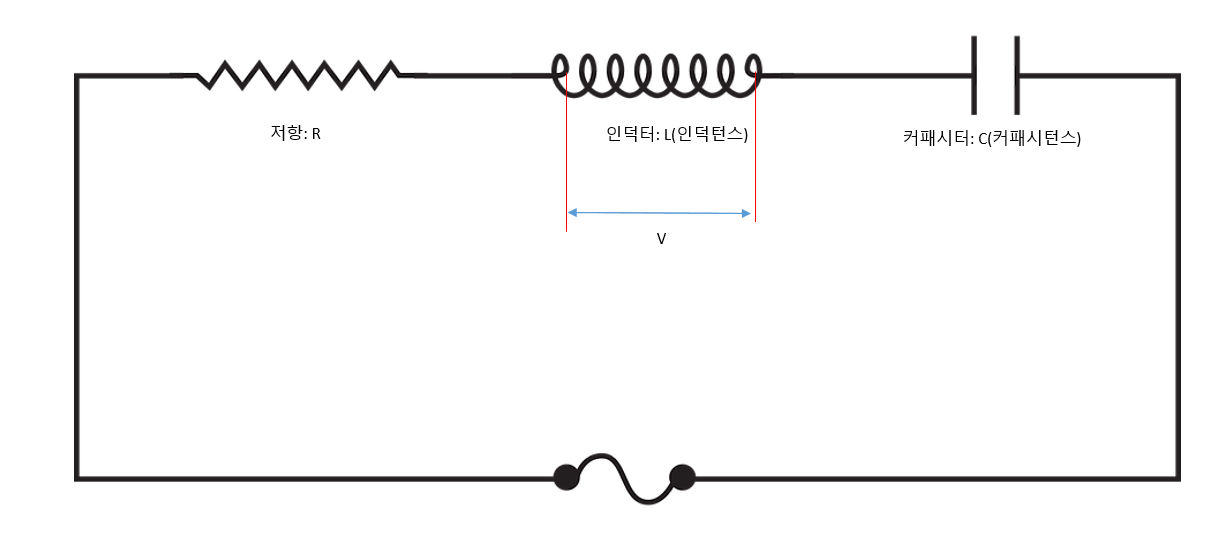
원래는 RL회로는 이렇게 생겼을 겁니다.

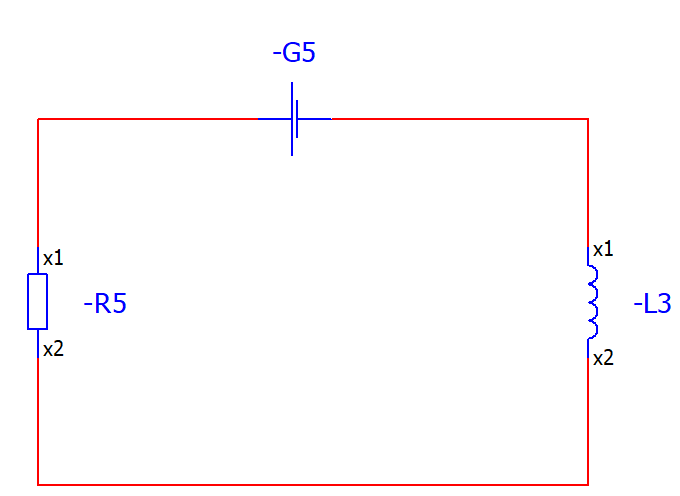
G5가 원래는 전위를 형성하여

R을 거치고 L에 전류를 통해주는 상황에서

G5가 끊어졌을때의 상황을 공부하는 것은(무전원 RL 회로를 배우는 목적).

앞으로 수많은 전기제품에서 이러한 현상이 응용되어 활용될 예정이며,

실제로 이러한 원리가 활용되는 제품을 접했을 때

우리는 이러한 현상을 수식으로 배움으로써

보다 깊은 지식을 흡수할 수 있습니다.

원래 전공서적들을 보면 냅다 수식부터 해석합니다.

아니요. 저는 그렇게 안하겠습니다.

여러분들이 전공서적을 보고도 제 글을 읽고 있는건 여러가지 이유가 있겠으나

그중 하나가, 책이 잘 이해가지가 않아서

공부차원에서 읽는 것일테니...

무전원 RL회로란건

우리가 지금까지 배웠던 V = I * R로 해석될 수 있습니다.

아니요.

정확히 말하면 V = I * Z로 해석될 수 있습니다.

R과 Z가 무슨차이냐고요??

R은 저항(OHM)

Z는 저항, 인덕턴스, 커패시턴스(OHM, HENRY, FARAD)

V = I * R 의 상황이라면

전원이 인가된 회로에서 갑자기 전압원을 뺏을때 상황이 그닥 의미가 없어요,

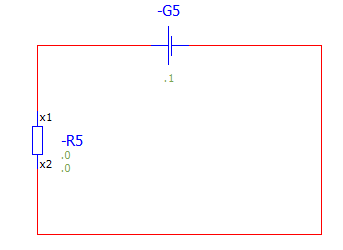
단순하게 생각해보세요.

G5 전압원이 전기를 주다가 갑자기 뺏습니다.

G5가 사라집니다.

잠시라도 R에 흐르는 전류가 있나요?

V = I * R 옴의 법칙에 의하면

V가 사라지면 I = 0입니다.

근데 저항 R이 아니라 여기에다가

임피던스 성분중 하나인 L과 C 좀 다르다는 겁니다.

V = I * R이 아니라

V= I * Z를 적용해야 하거든요.

우리가 기존에 배웠던 공식

V = L * dI / dt

Q = C * V

라는 특수한 성질 때문에

전압원을 끊어도 미세한 전류가 남아있는 시간이 아주 잠시동안 있다는 거에요.

그래서 우리는 무전원 RL 회로 무전원 RC 회로를 배우는 겁니다.

그 미세한 전류가 아주잠시 남아있는 시간동안

쌓여있는 에너지를 활용하여

수많은 반도체 및 로봇을 개발하였거든요.

V = L * di / dt

라는 공식에서 알 수 있듯이

시간의 따른 전류 변화는 1차 함수 그래프로 나타낼 수 없습니다.

저항은 그게 가능했지만요.

Q = C * V도 마찬가지에요

Q를 시간에 대해 미분하면 전류가 나옵니다 (Q = I * t)

그러면 위 수식을 시간에 대하여 양변을 미분하면

I = C * dV / dt

커패시터 역시도 시간과 전류의 그래프가 1차 함수 그래프로 나타낼 수 없습니다.

저항은 그게 가능했지만요!

여튼 이러한 성질때문에

전압을 끊어도 아주 잠깐 동안은 RL 회로 및 RC 회로에는 전류가 남아있을 수 있습니다.

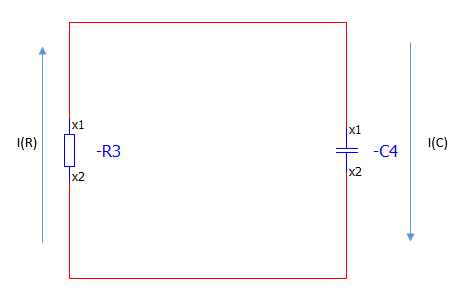
우리는 무전원 RL 및 무전원 RC 회로에서

전원을 갑자기 끊었을때

전류가 어떠한 형태로 떨어지는지가 궁금해서

미분방정식을 풀이하는거라 보시면됩니다.

수식정리를 지난 강의에서는 했는데

포스팅을 시작한 본질이 좀 흐려지는거 같아서

이번에는 무전원 RL회로에 대한

수식정리를 하지 않았습니다.

사실 포스팅을 진행하며 여러분들이 어떤 부분들이 궁금할지를 끊임없이 고민하고 올리는데

피드백이 없어서

수식에 대한 이해가 고픈건지

개략적인 이해가 고픈건지 잘모르겠습니다 ㅎ.

수식정리 부분에 대한 이해가 어려우신 분들은

피드백 주시면

향후 포스팅에서 수식관련된 부분도 함께 다뤄보도록 하겠습니다.

고맙습니다.

우리는 지금까지,

모든 전기회로에서 흔히보이는 보이지 않는 아주 기초적인 부품

저항, 커패시터, 인덕터 (수동소자)와

연산증폭기 (능동소자)

에 대해서 공부했었습니다.

지금부터는,

배웠던 기초들이 서로 결합될 때

어떻게 응용할 수 있고,

실무에 어떻게 적용되는지 알아볼 시간입니다.

사실 우리가 사용하는 휴대폰 및 컴퓨터에는

모두 인덕터, 커패시터, 저항등이 존재합니다.

수많은 인덕터, 커패시터, 저항등이 적절하게 배열되어

비로소 반도체가 될 수 있고, 이것을 잘 응용하면

비로소 컴퓨터와 휴대폰이 될 수 있는 것이죠.

대체 어떻게 저항 커패시터 인덕터를 조합하여 휴대폰을 만들 수 있었는지

어떻게 이것이 훗날 컴퓨터가 될 수 있었는지 궁금하지 않으세요?

물론, 이 몇개의 포스팅으로 반도체의 원리, 컴퓨터의 원리를 밝힐 순 없으며,

저 또한 모든 회로의 동작을 100% 이해하고 있지는 않습니다,

다만,

우리는 이번챕터를 공부하게 됨으로써 어떤식으로 부품(R, L, C)을 조합해야 내가

원하는 방향대로 전기를 통제할 수 있는지 배울 수 있을 겁니다.

학생 여러분이라면 여러분이 현재 배우는 이지식이 훗날

관련 분야에 취업하여 실무에 투입 되었을때 큰 도움이 될 것이라 확신합니다.

우리가 오늘 본격적으로 배워 볼 것은 전원이 없는 RC 회로입니다.

다만 여기에 약간의 상황을 가정한뒤 설명을 진행할 예정입니다.

커패시터는 C4는 전기를 저장할 수 있다 하였습니다.

우리는 이 소자에 초기에 에너지가 저장되어 있다고 가정하고

회로를 해석해 볼 겁니다.

"그렇담 이런 무전원 RC 회로가 과연 언제쓰일까?"

궁금증이 생길 수 있겠죠?

무전원 RC 회로는 사실 어떠한 목적을 가지고 만들었다기 보다는

직류 전원이 갑자기 끊어질때 발생하는데요.

예를 들어 이런겁니다.

그림을 보면,

G4는 자연스레 R4에 전기를 공급하며 열을 발생하며 에너지를 소비하고 있고,

G4는 자연스레 C5에 전기를 보냄으로써 에너지를 충전하고 있습니다.

(위 회로가 이해가 안가시는 분은 지난 포스팅을 참고해주세요)

여기서 전압원인 G4 가 어떤 이유에서건 끊어진겁니다.

그러면 이런 그림이 나올겁니다.

초기에 전기를 공급했던 전압원이 존재했기에

위 커패시터는 양단에 전압이 형성될 수 있습니다.

전압원이 없고 모두 수동소자인데 전압이 있다니 이상하죠?

비정상적인 상태는

정상적인 상태로 돌아가려는게 자연의 이치입니다.

때문에 C4에 존재하는 전압도 언젠가 소멸할 것이라는 자연스런 생각이 듭니다.

헌데 어떻게 소멸될까요?

지난 포스팅에서.

좀 오래되긴 했네요.

저항은 전기의 흐름을 막는 거라고 설명드린 적 있었죠.

엄밀히 말하면 전자가 이동할때 양성자와 부딪혀 에너지를 잃게 되는데.

그때 에너지 손실량이 열로써 나타나게 됩니다.

여러분이 집에서 쓰는 전기난로 자동차에 있는 엉따.

모두 같은원리에요.

다시 본론으로 돌아와서.

우리는 위 그림을 보면서 아래와 같이 사고 실험을 해볼 수 있을겁니다.

사고 실험

1. 전원이 차단된 직후 C4에 초기 전압이 존재할 것이다.

2. 하지만 C4 전압은 곧 소멸될 것이다.

3. R3 저항이 열로써 모두 에너지를 소모할 것이니까.

말로써는 그럭저럭 이해가 가는데 수학적으로도 그런지 한번 볼까요?

사고 실험 1번에 가정했던 C4 초기 전압을 V(0) 라고 가정해볼게요

키르히호프 법칙을 적용해보겠습니다.

폐루프를 회전하는 전류의 합은 항상 0이다.

때문에

아래 수식이 성립합니다

I(R) + I(C) = 0

여기서

I(R)은 V(0) / R 로 표현할 수 있고

I(C)는 Q=C*V 공식에서 양변을 시간으로 미분해

I(C) = C* dV/dt 를 구한뒤

대입하면 됩니다.

정리하면,

v(0) / R3 + C * dV / dt = 0

인건데요.

여기서 의미하는 수식이 잘 이해가 되지 않으니

약간의 수학적인 테크닉을 통해서 수식이 의미하는 바를

알아챌 수 있게 끔 깔끔하게 만들어 볼게요.

위 수식은 잘 정리하면 아래와 같습니다.

dV / v(0) = -{1 / (R*C) * dt}

양변을 시간으로 적분해볼게요

ln(v) = -t / (R*C) + ln(A)

이걸 더 정리해보면

ln(v / A) = -t / (R*C) .... 수식 1

(이 수식이 이해가 가지 않는 분들은 공학수학을 배우셔야 하는데, 사실 시험볼

목적이 아니라면 모른다고 좌절하지 마시고 수식유도는 가볍게 읽고 넘어가시면 됩니다.)

여기서 수식1을 지수함수로 표현을 해볼게요

v(t) =  A*e^(-t / R*C)

근데 v(0) 즉 무전원 RC 회로에서 전원을 차단했을때 전압이 V(0) 이니까

A = V(0)

더 수식을 정리하면,

v(t) = V(0)*e^(t / R*C) ..... 결론

겁나 어렵고 이해도 안가고...

왜 이렇게 복잡하게 난리를 피웠냐구요?

우리는 수많은 수식 삽질끝에

비로소 위 수식을 시간과 전압 그래프로 나타낼 수 있는 수식을 얻었는데.

사실 사고 실험에서는

시간이 지나면 전압이 저항의 열로 소멸될 것이라는 추론만 가능했는데

수식으로 표현하니 어떻게 전압이 변화하는지 구체적으로

시간을 알 수 있게 되었습니다.

내가 궁금했던. 아니. 그러니까 여러분이 궁금하지 않아도 알아야 하는 이 장황한 수식은

바로 무전원 R, C 회로에서 어떻게 전압이 시간에 따라 변화하느냐를

나타내는 디테일한 지침인겁니다.

수학적으로요.

위 그림은 여러분이 앞으로 전장 설계를 맡게 되었을때

소자의 특성을 그래프로 나타낸 기술적인 특성을 확인할 수 있도록 표현한 Datasheet 인데요.

RC 필터에서 나타나는 저 지수함수와 같이

대부분의 차단기 밑 RC 필터는

이렇게 지수함수 모양을 하고 있습니다.

실제로 엔지니어로 일하게 되면, 저렇게 디테일한 부분까지는 몰라도 되지만.

원리정도는 알고 있어야 엔지니어로써 역량이 더 성장할 수 있겟죠?

포스팅이 길었네요.

저는 이만 물러가고

다음 포스팅에 또다른 회로를 들고 나타나도록 하겠습니다.

지난 시간에

인덕터라는 것은

전선을 동그란형태로 말아놓은 것이라고 말씀드렸죠.

그리고 중요했던 포인트.

인덕터는 전압과 전류의 관계에 있어서

옴의 법칙내 R과 같은

무언가라고 설명 드렸습니다.

자 주제를 살짝 넓게볼까요?

우리가 배웠던 3가지

수동소자.

1. 저항(Resistor)

2. 커패시터(Capacitor)

3. 인덕터(Inductor)

V = I * R

Q = C * V

(Q = I * t)

V = L * (di / dt)

우리가 지금까지 열심히 배웠던 위 3가지 수식이 모두

전압과 전류사이를 규정함에 있어서 어떠한 상수값으로 표현될 수 있다는 내용이었습니다.

우리는 전압과 전류관계에 있어서 그 사이 상수값을 결정하는 R, L, C를

한곳으로 묶어서 임피던스(Impedence)라고 표현합니다,

보시다시피 회로이론은

전기의 근원인 전압과 전류라는게 어떻게 형성되는지

지구상에 어떤 물질로 전기를 활용할 수 있는지를

공부하는 가장 기초적인 학문입니다.

제가 인덕터 파트에서 지금과 같이 전체를 한번 묶어 설명하는 이유는

앞에서 배웠던 것과 지금 배우는게 어떤 연관성이 있으며,

이걸 왜 배워야 하는지를 큰 시각으로 말씀드리는 부분입니다.

우리는 임피던스라는 것을 이해하게 되었을때,

비로소 적재 적소에 전압과 전류를 제어할 수 있다는 것을 의미합니다.

전압과 전류는 그사이 상수(R, L ,C)로 부터 결정되기 때문이죠.

지금까지 배운 지식들의 목적.

우리는 이러한 특성을 익힘으로써

회로를 설계하든 보드를 설계하든 반도체를 설계하든

중요한 밑거름 지식을 얻게 되는겁니다. 

본론으로 돌아오겠습니다.

일전의 포스팅에서 저항을 직렬과 병렬로 연결했을때

어떤 변화가 있었는지 기억하시나요?

저항은

직렬로 연결하면 그 값이 더해졌었고,

병렬로 연결하면 그 값이 역수값으로 계산됬었죠.

기억이 잘 나지 않는다면,

저항의 직렬 및 병렬연결 포스팅을 리뷰하시기 바랍니다.

인덕터 역시

저항의 합성 공식과 완전히 동일합니다.

상식적으로 이해가 되실겁니다.

저항도 저항률이 큰 어떤 물질을 길게 늘여뜨려 놓은 것이고

인덕터도 동그랗게 말아 놓은 전선을 길게 늘여뜨린 모양이거든요.

해서 저항이나 인덕터는 각 제품을 직렬이나

병렬로 연결할때 동일한 특성을 갖습니다.

직렬연결

L(등가) = L1 + L2

병렬연결

1 / L(등가) = 1 / L1 + 1 / L2

우리는 이렇게

오늘까지 배운내용을 끝으로

실제 많은 전기전자 공학도들이

학교에서 배우는 회로이론 내용의 약 절반을 마쳤습니다.

보통은 여기까지 하고 중간고사를 봤었죠.

이후부터는. 

우리가 배웠던 소자들을 가지고 회로를 구성할때

회로가 어떻게 해석되는지.

전류와 전압과 임피던스의 관계가 어떻게되며

어떠한 용도로 그러한 회로를 활용할 수 있는지를 배워나갈겁니다.

회로이론 파트는 사실. 포스팅하기가 참 어려운 부분이 많네요.

여튼. 몇번 거르더라도 꾸준히 포스팅할테니

열공해주시길 바라며 전 이만 물러가도록 하겠습니다.

지난시간에 이어

오늘도 인덕터 관련된 이야기를 들고 왔습니다.

지난 시간에 전선을 철심에 동그란 모양으로 말아서

전류를 흘리면

수직하는 방향으로 자기장이 형성된다 했었죠?.

전류와 자기장의 존재는 매우 중요한 의미를 지닙니다.

서로의 상관관계가 있기 때문인데요.

우리는 전류를 흘려서 파란색 화살표와 같이 자기장을 얻을 수 있었지만

반대로 자기장을 가해서 없었던 전류를 만들어 낼 수도 있습니다.

자속의 변화로 인해 전기를 만들어내는게 바로 발전기이고요.

반대로 전기를 흘려서 자기장을 발생시켜 힘이 발생하면

이것을 이용하여 모터로 활용할 수 있습니다.

이 얘기는 초보자들이 이해하기 조금 어려울 수 있으므로 이후 전기기기나

실무지식을 소개하면서 더 자세하게 말씀드리도록 하겠습니다.

여튼 자기장과 전기 발생에 대한 상관관계에 대해서는

 이후에 배울 패러데이의 법칙에 이러한 내용이 나옵니다.

하지만 그전에 우리는 인덕터 자체에 대해서 더 깊게 공부해보겠습니다. 

 얘기가 샜네요.

다시 인덕터를 깊게 알아보죠.

먼저 인덕터는 아래와 같은 수식을 만족합니다.

V 는 전압

L 은 인덕턴스

t 는 시간

i 는 전류

입니다.

수식을 그대로 해석해보면.

전류의 변화량이 클수록,

인덕턴스가 뭔진 모르겠지만. 값이 클수록

전압이 크게 형성됩니다.

직관적으로 이해 가능하듯

여기서 말하는 전압이란

코일의 시작점(코일이 말리기 시작하는 시작점)

으로부터

코일의 종점(코일이 말리고 다시 평평하게 펴지는 지점)

까지 

걸리는 전압을 말합니다.

위 그림보면 각각 소자가 어떤 것인지 이해하실 수 있으시겠죠?

모두 배운 소자들이긴 합니다.

몰랐다면 지금부터 익혀두세요.

여기서 앞서 배운수식

전압은 인덕터의 양단에 걸리는 전압을 말합니다.

그러니까. 그림으로 표현하자면 아래 같겠네요.

      이상한거 없나요?

이쯤이면 이상한 걸 느꼇어야 했습니다.

뭐가 이상한걸까요???

저는

인덕터를 전선을 말아놓은 것에 지나지 않는다고 말씀드렸죠.

네.

그렇습니다.

인덕터는 저항성분이 없습니다.

단순히 전선을 동그랗게 말아놓은 것에 지나지 않으니까요.

그래서 이상하다는 겁니다.

커패시터처럼 전기를 저장하는 소자도 아닌데

저항이 존재하는 것도 아닌데

단순히 전선을 펴놓치 않고 동그랗게 말아놨을뿐인데

여기서 말하는 전선은 이상적인 형태(저항이 0에 가까운 전선)을 말합니다

왜 전압이 있단말입니까?

옴의 법칙에 의해서 (V = I * R)

전압과 전류가 존재하는 현재 상황으로 미루어봤을때

 R에 해당하는 어떠한 미지 상수가 존재해야 하거든요?

근데 인덕터 수식을 딱보니

L(인덕턴스) 라는 것이 바로 그역할을 하는것 같습니다.

단순히 전선을 동그랗게 말아 놓았을 뿐인데

미지의 저항상수 L이 생긴겁니다.

L은 인덕턴스라고 표현하며, 단위는 인덕턴스를 발명한 미국의

과학자 이름을 따서 (H)헨리 라고 표현합니다.

무튼 이러한 인덕턴스로 인하여 전압은

전류의 변화를 거부하는 방향으로 형성됩니다.

즉 코일에 전기가 흐르지 않다가

갑자기 흐르게 되면

갑자기 흐르는 이런 부자연스러운 현상을 제거하기 위해

마치 전류가 반대방향으로 흐르게 끔 만들어서

실제 전류의 방향을 상쇄하게끔 전압을 준 효과(역기전력)가 나타나는거죠

그래서 인덕터가 많은(유도성 부하라고 표현합니다) 전력계통은

실제로 전압이 많이 떨어집니다.

왜 하필 정기전력이 아니라 역기전력이 생기냐는 질문은 조물주께 여쭤보시기 바랍니다

(자연의 이치이며 공리라고 표현합니다.)

이러한 인덕터는 커패시터와 혼용하여 역률을 개선할때 쓰이기도 하며

또다른 중요한 특성때문에 여러가지 목적으로

설계에 응용됩니다.

자꾸 수식을 끌고오지만 다시 수식을 한번 살펴보면

역기전력이 전류의 시간변화율에 따라 생기므로.

보통 직류에서는 역기전력이 생기지 않아요.

네 맞습니다. 교류에서만 역기전력이 생깁니다.

추가로 전류는 급격한 시간에 변화할 수 없다는 사실을 아는게 중요합니다.

시간에 따라 전류가 급격하게 변화한다는 것은 위 수식에 따라

전압이 무한대로 갈 수도 있다는 것을 의미하죠.

하지만 현실에선 이런일이 일어나지 않습니다.

이러한 성질로부터 과전류를 보호할 수도 있고

이후에 배우겟지만 용량성 부하로부터 역률을 개선시켜 제품 자체의 효율을 높일 수도 있습니다.

사실 비전공자는 인덕터가 실생활에서

보이지 않다보니

이번 챕터는 조금은 어렵기도 했겠군요.

복잡한 수식이야 책에서도 지겹도록 보실테니

머리로 이해할 수 있도록 쉽게 설명하고자 하는데

아무래도 좀 이번챕터가 복잡하긴 했네요.

여튼... 오늘도 고생많으셨습니다.