'전기공학 기초이론'에 해당되는 글 57건

오늘은 커패시터에 이어 또다른 에너지 저장소자인

인덕터에 대해 배워보겠습니다.

인덕터는 코일입니다.

둘둘 말려있는 구리선이

바로 인덕터인데요.

왜 구리선을 직선으로 말아가지고 쓰는 것이냐?

바로. 자기장을 이용하기 위해 그렇습니다.

자기장을 이용하는 방법은 매우 간단합니다.

둥그렇게 전선을 말아놓고 전기만 흘리면 자기장이 생기거든요.

네이버 백과사전에

오른나사의 법칙을 쳐보면 이런 그림이 나옵니다.

이 그림이 설명하는 바는 간단합니다.

도선에 전류를 흘리면 위 그림처럼 자기장이 형성된다는 겁니다.

자기장이 왜 생기느냐에 대한 궁금증은 밝힐 수  없습니다.

자연현상이기 때문이죠.

[자연현상에 대한 이유는 신이 존재한다면. 신만이 알 겁니다.]

자연계에 살아가는 우리는 자연계의 현상을 규명하기보다는

자연계의 현상을 응용하여 실생활에 이롭게 하는 것을 목적으로 공학이라는 분야를 만들었으므로 

자연현상을 그대로 받아들여야 합니다.

다시 본론으로 돌아와서.

도선에 전기를 흘리면 위와 같이 자기장이 형성되는 원리를 바탕으로 인덕터를 만들었는데요.

인덕터의 구조대로 전기를 흘리면 어떻게 자기장이 형성될까요?

위 그림의 화살표 방향대로 전류를 흘린다고 가정해보겠습니다.

도체에 전류를 흘리면 자기장이 형성된다는

오른나사의 법칙을 알았으므로 자기장의 형성방향 또한 추측할 수 있습니다.

헌데 좀 특이한 것이 보입니다.

각 지점마다 전류를 흘리는 방향을 오른나사의 법칙을 적용해보았더니

한쪽 방향으로 자기장이 강해지는 모습처럼 자기장이 형성된다는 것이죠.

도체에 전기를 흘렸더니 실제 자석처럼 자성이 생겼습니다.

말로는 이해가 안가니 아래 그림을 보죠.

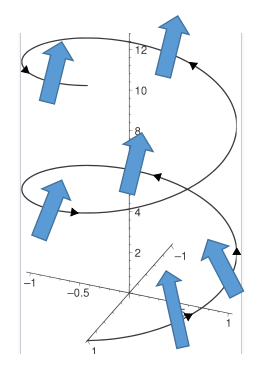
위 그림에서 검은색 화살표는 전류의 방향을 표현하고

파란색 화살표는 자기장의 방향을 표현하였습니다.

도선의 방향대로 오른나사의 법칙을 적용하여 자기장의 방향을 보았더니

조금 삐뚤 빼뚤하지만

어느정도 한방향을 가르키고 있구나 라는 사실을 모두가 직관적으로

알 수 있습니다.

설명을 위해 나선간의 폭이 매우 큰것처럼 표현했지만

아주 촘촘한 나선이라면 어떻게 자기장이 형성되겠습니까?

자기장이 형성되는 방향은 코일 내부에서

거의 직선이 되는겁니다.

결국 인덕터는

전선을 동그랗게 촘촘하게 말아놓은 것인데

단순히 도체와는 다르게

자기장이 한쪽방향으로 강해지게끔

하드웨어적인 조정이 이루어진 기구라고 보시면 됩니다.

우리 선대 과학자들 및 공학자들은

이러한 자기장을 이용하여

다양한 전기기기를 발명하였습니다.

모터뿐만 아니라 반도체 휴대폰등

모든 전자기기에 위 원리가 포함되어있습니다.

여러분이 휴대폰을 연구하는 사람이라면

여러분이 자동차를 연구하는 사람이라면

여러분이 컴퓨터 하드웨어를 연구하는 사람이라면

내부의 구성 요소정도는 이해해야 하고

우리는 그래서 인덕터를 배우는겁니다.

인덕터가 어떤 것인지 이해했으니 다음 시간부터는

인덕터가 전기회로에서 어떻게 사용되고

어떤 성질을 가지고 있는지 본격적으로 알아보도록 하겠습니다.

꽤 오랜 포스팅동안 

커패시터에 관한 이야기를 했습니다.

커패시터가 그만큼 중요하기 때문이고 회로설계 및 해석에

중요한 개념이기 때문인데요

오늘은 지난시간에 이어서 커패시터가 여러개가 붙어있는 경우

어떻게 회로가 해석될 수 있는지

알아보도록 하겠습니다.

우리 이전시간에 저항을 직렬로 연결했을때와 병렬로 연결했을때

특징을 알아본적 있었습니다.

저항은

직렬로 연결할수록 그 값이 커지고,

병렬로 연결할수록 그 값이 작아진다.

저항과 같이 커패시터도 하나의 소자로써

이를 연결하는 방법에 따라 직렬 연결과 병렬 연결로 나뉘는데요.

특이한건. 저항과 다르게 커패시터는

직렬로 연결하면 그 값이 작아지고,

병렬로 연결하면 그 값이 커진다는 것.

여기서 말하는 값이라는건. 커패시턴스

즉, 지난시간에 배운 공식

Q = C*V 에서

C를 의미합니다.

저항이 직렬로 연결할수록 R 값이 커지는 반면

커패시턴스 C는 직렬로 연결하면 C 값이 작아지고

저항이 병렬로 연결할수록 R 값이 작아지는 반면

커패시턴스 C는 병렬로 연결하면 C 값이 커집니다.

이유가 궁금하죠?

왜그럴까요?

회로도를 봅시다.

커패시터를 직렬로 연결하면 대략 이런 모습이겟죠.

보면, C1에 양전하가 몰려있고

C3에 음전하가 몰려있죠.

자그럼 C2는 어떤가요?

C2는 양 극단에 전압원이 존재하지 않는 허당 커패시터입니다.

직렬로 연결하고 보니 무슨 일이 벌어졌냐면.

C1, C2, C3 각각 전기를 저장할 수 있는 능력이 충분함에도 불구하고

허당 커패시터가 생긴더라는 거에요.

더군다나 전기를 저장할 수 있는 공간 총 6개 중 무려 4개가 허당이 되었습니다.

쉽게말해서

C1에 저장할 수 있는 전하가

10개

C2에 저장할 수 있는 전하가

10개

C3에 저장할 수 있는 전하가

10개면

이중에 3/2는 허당이되는겁니다.

총 30개의 전하를 저장할 수 있는 전하 저장능력이

직렬로 붙였더니 10개가 되었다는 뜻이죠.

설명을 위해 직관적으로 말씀드린 부분이지만.

선대 과학자가 밝혀낸 사실에 의하면

커패시터는 아래와 같은 성질이 있다는 것이 실험적으로 증명되었으며 

1/C1 + 1/C2 + 1/C3 = 1/C(total)

이는 수학적인 증명도 가능합니다.

Q = C*V 라는 수식을 봅시다.

위 회로상에

C1에서 발생한 전압

C2에서 발생한 전압

C3에서 발생한 전압

그리고 G2의 전압의 합은 0이어야 하죠.(키르히호프 전압법칙)

-G2 + V(C1에 걸리는 전압) + V(C2에 걸리는 전압) + V(C3에 걸리는 전압) = 0이라는 거죠.

헌대 V(C1에 걸리는 전압)은 다른 방법으로 표현 가능합니다.

Q = C * V 라는 공식을 통해서 말이죠 

V = Q / C 으로 표현할 수 있죠.

이를 대입하면 수식은 아래와 같이 나타낼 수 있어요

Q / C1  + Q / C2  + Q / C3 = Q / C(total)

여기서 다시 양변을 Q로 나눠보면 이런 수식이 나옵니다. 

1 / C1  + 1 / C2  + 1 / C3 = 1 / C(total)

쉽죠?

병렬로 연결하는 경우는 더 쉬워요 직관적으로 이해하기 더 쉽거든요

병렬이란 뜻은 아래와 같은 회로 표현이 가능할겁니다.

그림을 보세요.

C1, C2, C3 .... 쭉쭉 붙여나갈수록

+가 위치할 수 있는 공간이 늘어나고

-가 위치할 수 있는 공간이 늘어납니다.

그래서 병렬연결에서 커패시턴스의 관계식은 이렇습니다

C1 + C2 + C3 = C(total)

끝이네요.ㅎ

다음 시간에는 커패시터 만큼 중요한

인덕터라는 소자에 대해서 알아보겠습니다.

즐거운 한주 마무리하세요

오래간만입니다.

개인적으로 2022년 많은 일들이 있어서 오래동안 포스팅을 쉰점

독자 여러분들께 깊은 양해를 구합니다.

바로 포스팅 시작하도록 하겠습니다.

캐패시터는

전기를 마치 저장하는듯 보입니다.

양극판에 모인 양전하와 음전하가 닿을듯 말듯한 거리에서 서로를 인력으로

끌어당기고 있기 때문이라고

지난 포스팅에서 설명드린 바 있죠.

일반적으로 캐패시터가 전기를 저장할 수 있는 이유는

음전하와 양전하가 만날 수 있는 길이 없기 때문입니다.

이게 무슨소리냐.?

그림1을 보자면.

한쪽 극판에는 '+' 가 쌓이고

나머지 다른 극판에는 '-' 가 쌓입니다.

지금까지는 전압원이 큰힘으로 양전하와 음전하를 극판에 모아주었죠.

전압원이 없다면 음전하는 양전하와 만나기위해 다음과 같이 곧장 경로를 틀겠죠.

아래처럼요

근데 전압원이 있다고 했을때 왜 전자는 위 그림처럼 이동하지 않느냐???

전압원이 존재할 경우 음전하가 양전하와 만날 수 없는 이유는

전자가 양전하를 만나려는 힘보다 전압원이 극판으로 밀어내는 힘이 훨씬 강하기 때문이죠.

즉, 엄청나게 큰힘으로 전압원이 밀어주고 있기 때문입니다.

만약 큰힘의 전압원이 사라지고

극판에 모여있는 양전하와 음전하가 서로 만날 수 있는 더 쉬운 방법이 생겼다고 하면, 어떻게 되겠습니까?

그림 2처럼요

전자는 양전하와 만나기 위해 이동할 겁니다. 

그럼 어떻게 되겠습니까?

그림 3처럼 X1 부분에 전자가 몰려서 중성이 되다보니

상대적으로 X2 부분이 양전하가 많이 생기지 않겠습니까?

그럼 어떻게 될까요? 다시, 전하는 반대방향으로 이동하겠죠

이상적인 커패시터는 이렇듯

전자가 끊임없이 충전과 방전을 진행합니다.

이때 중요한건 이겁니다.

전자가 이동하기 때문에 커패시터는 전류와도 관계가 있는데

커패시터와 전류의 관계는 과연 무엇이냐!?

 10년전 기억이라 가물가물 하긴하지만

천천히 되새겨보면

Q = C * V

라는 공식이 있습니다.

여기서

Q는 전하량을 의미하고 C는 커패시턴스 V는 전압입니다.

여기서 한가지 더 짚고 넘어갈게 있는데요.

전하량과 전류의 관계입니다.

전하량을 시간으로 미분한다는 것은 시간과 전하량의 그래프를 그렸을때 기울기와도 같은데

시간 전하량 그래프에서 기울기는 전류를 의미하거든요

반대로 생각하면, 전류를 시간에 대해 적분하면 전하량이 나옵니다.

직관적으로 이해하시면 이해갈겁니다.

전류라는게 전하의 이동을 나타내는 단위이고, 전하의 이동이 얼마만큼의 시간동안 이루어졌느냐를

나타내는 총량이 전하량 Q라고 생각하시면 쉽겠네요.

시간 속도 거리의 개념과도 같습니다. 

1초에 10미터를 달리는 A가 10초를 달렸다고 하면 100m를 달린거죠

1초에 2만큼 움직이는 전하가 10초만큼 지났다 하면 총 20개의 전하가 흘렀겠죠.

이때 1초에 2만큼이라는 게 바로 전류

10초가 시간

20이 전하량입니다.

다시 돌아와서

Q = C * V

양변을 시간으로 미분 하면 다음 관계가 성립합니다

자 이 수식에서 우리가 생각할 수 있는게 뭔지가 레알 중요한데

잘 생각해봅시다

전압이 시간에 따라 일정한게 직류전압이란 얘긴 예전에 이미했을겁니다.

직류에선 전압이 시간이 지나도 전압이 변화하지 않으므로 전류는 0이 될 수 밖에 없어요

왜냐면 직류전압이 dV / dt = 0이거든요

한마디로 커패시터는 직류전압에서는 개방회로로 동작한다는 의미입니다.

"뭐야 그럼 그림 1은 실질적으로 커패시터가 있으나 없으나 전류가 안흐른다는 뜻이네?"

네 맞아요.

흐르지 않습니다.

직류는 시간의 변화에 따른 전압의 변화가 없으므로(실제로는 약간 있습니다. 그래서 미세하게 전류가 흐릅니다.)

전류는 흐르지 않습니다.

하지만 V1을 치워버리는 순간 극판의 +, -는 위에 설명했듯 무한반복 되는겁니다(이상적인 경우)

또중요한거 하나.

커패시터에서 전압은 갑자기 휙바낄 수 없어요.

수식만봐도 얼추 알 수 있죠

전압이 짧은시간내에 휙바뀐다는 것은

전류인 i 가 무한대까지도 갈 수 있다는 뜻 입니다.

전류가 무한대일 수 가 있나요?

네 없습니다.

그런일은 벌어지지 않습니다.

이 2가지를 기억해야됩니다

커패시터는

1. 전압이 갑자기 변하지 않는다.

2. 커패시터는 직류 회로에 대해 개방회로로 동작한다.

오랜만에 티스토리 포스팅을 시작하니

포스팅이 다소 무거워진 느낌입니다.

설명도 쉽게한다고 하는데 의미전달이 제대로 되었는지 모르겟네요.

여튼 다음 포스팅에서 이러한 커패시터들이 직렬 또는 병렬로 연결되었을때

어떠한 계산으로 값이 계산될 수 있는지 알아보도록 하겠습니다.

지난시간에 커패시터가 뭘 의미하는지 간략하게 알아보았습니다.

커패시터란 전기를 충전하고 방전하는 기능을 수행하는 것으로,

전자회로에 수 많은 커패시터가 사용되며

실생활 응용 예중 가장 밀접하게 접할 수 있는 부분을 꼽으라면.

우리가 반도체물성에서 배웠던 반도체에서도 커패시터가 엄청나게 많이 사용됩니다.

우리는 지난시간에

커패시터의 기본 공식에 대해서 배웠었죠

Q = C * V

위 공식에서

Q는 전하량

C는 비례상수이며 커패시턴스라고 불립니다.

V는 전압이고요.

전하량이 전압과 비례한다는 의미입니다.

전하량이라는 건

전자의 양을 의미하는데

전자가 쉽게말해서 얼마나 많이 저장될 수 있는지 그 능력이.

전압의 크기와

비례상수로 결정된다는 의미죠.

다시 말하면.

아주 상식적으로 생각했을때

전압이 전기적인 위치에너지를 나타내주는 것이므로

전기에너지가 크다면

전자를 많이 밀어낼 수 있겠죠.

외우려고 하지말고 아래와 같이 문장으로 읽어보면

너무 당연한 이야기입니다.

'전기를 저장하는 능력은 전자를 밀어낼 수 있는 힘에 의해 좌우된다.'

여기에 전자를 저장할 수 있는 요소가 한가지 더 있다면

그것을 바로 커패시턴스라고 부를 수 있는 것인데

커패시턴스는 물질마다 고유하게 정해져 있는 값입니다.

Q나 V가 변한다고해서 C가 변할 수 없어요.

C는 그렇다면 어떤것에 의존하는 것이냐?

C = (유전율 * 판의 넓이) / 판의 거리

이렇게 말해서는 이해가 당연히 안가겠죠.

아래 그림처럼 회로가 있다고 가정해봅시다. 

위 그림처럼 '+'가 모여있는곳, 그리고 '-'가 모여있는 곳을  입체적으로 확대 해보겠습니다.

외우지 마시고 한번 공식을 다시보세요.

C = (유전율 * 판의 넓이) / 판의 거리

C는 전하량을 저장하는 능력에 비례하는 비례상수로 쓰인다 했습니다.

C가 크다는 것은 전하량을 저장하는 능력이 좋다고 판단할 수 있고

C가 작다는 것은 전하량을 저장하는 능력이 안좋다고 판단할 수 있겠죠.

그런데 그런 C라는 값이 판의 넓이에 비례한다고 합니다.

판의 넓이가 커질수록 '+', '-'가 들어갈 수 있는 면적이 넓다고 자연스럽게 상상이 되십니까?

그렇담 거리는요?

거리가 가까우면 가까울수록 '+' , '-' 양전하와 음전하의 인력이 강해지겠죠.

때문에 더 충전이 잘된다고 판단할 수 있을겁니다.

여기서

ε라는 것은 입실론이라고 읽고.

어려운말로 유전율이라고 표현하는데

어렵게 생각할거 없습니다.

외부에서 적절한 자극을 주었을때

전기적인 성질을 가질 수 있는 확률이 얼마나 높냐 정도로 이해하시면 됩니다.

즉, 유전율이 크면 클수록 전기적인 성질을 띄기 쉽고

유전율이 작을수록 전기적인 성질을 가지기 어렵습니다.

유전율(ε)이 클수록, 면적의 크기(A)가 클수록, 극판의 거리(d)가 가까울수록

전하를 저장하는 능력(C)이 커지고

유전율(ε)이 작을수록, 면적의 크기(A)가 작을수록, 극판의 거리(d)가 길수록

전하를 저장하는 능력(C)이 작아집니다.

아래 공식이 성립하는 이유는 위 설명에서 찾을 수 있겟네요.

C = (유전율 * 판의 넓이) / 판의 거리

다음시간에 이어서 커패시터의 특징을 계속 설명드리겠습니다..