'회로이론'에 해당되는 글 21건

꽤 오랜 포스팅동안 

커패시터에 관한 이야기를 했습니다.

커패시터가 그만큼 중요하기 때문이고 회로설계 및 해석에

중요한 개념이기 때문인데요

오늘은 지난시간에 이어서 커패시터가 여러개가 붙어있는 경우

어떻게 회로가 해석될 수 있는지

알아보도록 하겠습니다.

우리 이전시간에 저항을 직렬로 연결했을때와 병렬로 연결했을때

특징을 알아본적 있었습니다.

저항은

직렬로 연결할수록 그 값이 커지고,

병렬로 연결할수록 그 값이 작아진다.

저항과 같이 커패시터도 하나의 소자로써

이를 연결하는 방법에 따라 직렬 연결과 병렬 연결로 나뉘는데요.

특이한건. 저항과 다르게 커패시터는

직렬로 연결하면 그 값이 작아지고,

병렬로 연결하면 그 값이 커진다는 것.

여기서 말하는 값이라는건. 커패시턴스

즉, 지난시간에 배운 공식

Q = C*V 에서

C를 의미합니다.

저항이 직렬로 연결할수록 R 값이 커지는 반면

커패시턴스 C는 직렬로 연결하면 C 값이 작아지고

저항이 병렬로 연결할수록 R 값이 작아지는 반면

커패시턴스 C는 병렬로 연결하면 C 값이 커집니다.

이유가 궁금하죠?

왜그럴까요?

회로도를 봅시다.

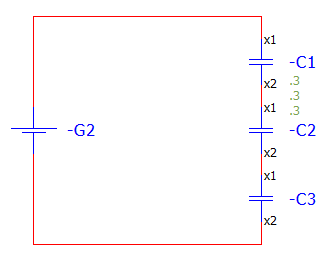
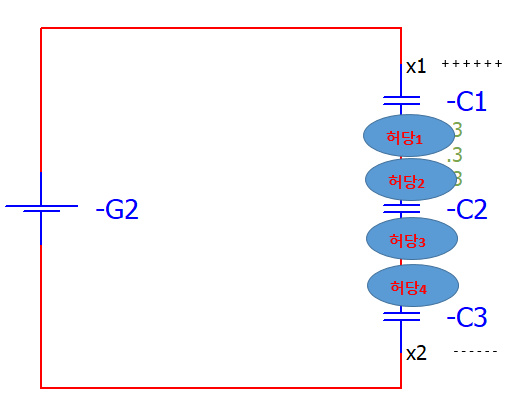
커패시터를 직렬로 연결하면 대략 이런 모습이겟죠.

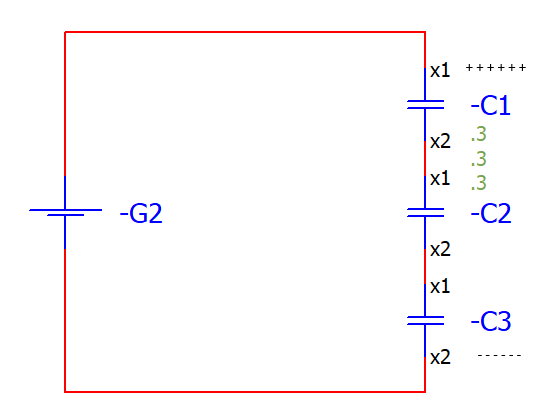
보면, C1에 양전하가 몰려있고

C3에 음전하가 몰려있죠.

자그럼 C2는 어떤가요?

C2는 양 극단에 전압원이 존재하지 않는 허당 커패시터입니다.

직렬로 연결하고 보니 무슨 일이 벌어졌냐면.

C1, C2, C3 각각 전기를 저장할 수 있는 능력이 충분함에도 불구하고

허당 커패시터가 생긴더라는 거에요.

더군다나 전기를 저장할 수 있는 공간 총 6개 중 무려 4개가 허당이 되었습니다.

쉽게말해서

C1에 저장할 수 있는 전하가

10개

C2에 저장할 수 있는 전하가

10개

C3에 저장할 수 있는 전하가

10개면

이중에 3/2는 허당이되는겁니다.

총 30개의 전하를 저장할 수 있는 전하 저장능력이

직렬로 붙였더니 10개가 되었다는 뜻이죠.

설명을 위해 직관적으로 말씀드린 부분이지만.

선대 과학자가 밝혀낸 사실에 의하면

커패시터는 아래와 같은 성질이 있다는 것이 실험적으로 증명되었으며 

1/C1 + 1/C2 + 1/C3 = 1/C(total)

이는 수학적인 증명도 가능합니다.

Q = C*V 라는 수식을 봅시다.

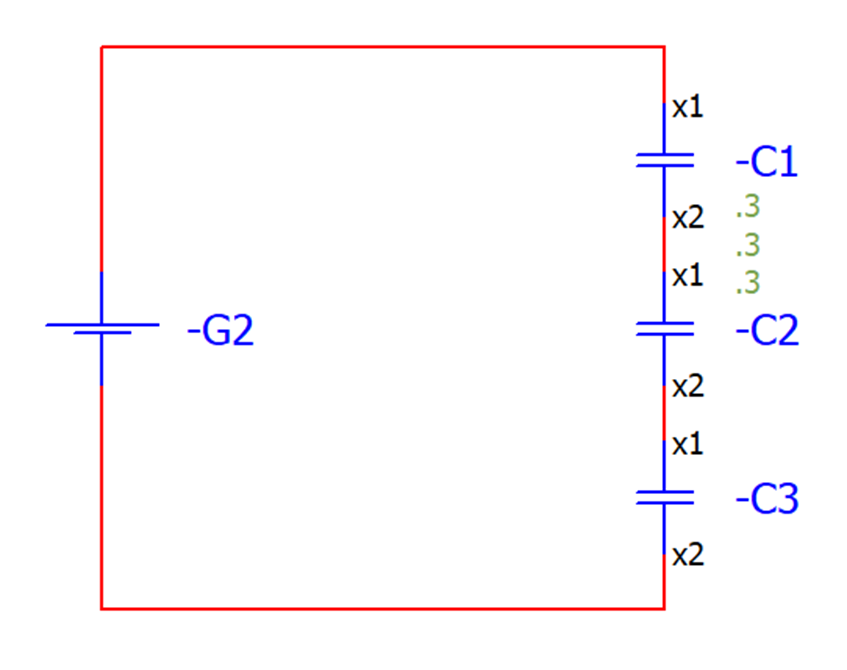
위 회로상에

C1에서 발생한 전압

C2에서 발생한 전압

C3에서 발생한 전압

그리고 G2의 전압의 합은 0이어야 하죠.(키르히호프 전압법칙)

-G2 + V(C1에 걸리는 전압) + V(C2에 걸리는 전압) + V(C3에 걸리는 전압) = 0이라는 거죠.

헌대 V(C1에 걸리는 전압)은 다른 방법으로 표현 가능합니다.

Q = C * V 라는 공식을 통해서 말이죠 

V = Q / C 으로 표현할 수 있죠.

이를 대입하면 수식은 아래와 같이 나타낼 수 있어요

Q / C1  + Q / C2  + Q / C3 = Q / C(total)

여기서 다시 양변을 Q로 나눠보면 이런 수식이 나옵니다. 

1 / C1  + 1 / C2  + 1 / C3 = 1 / C(total)

쉽죠?

병렬로 연결하는 경우는 더 쉬워요 직관적으로 이해하기 더 쉽거든요

병렬이란 뜻은 아래와 같은 회로 표현이 가능할겁니다.

그림을 보세요.

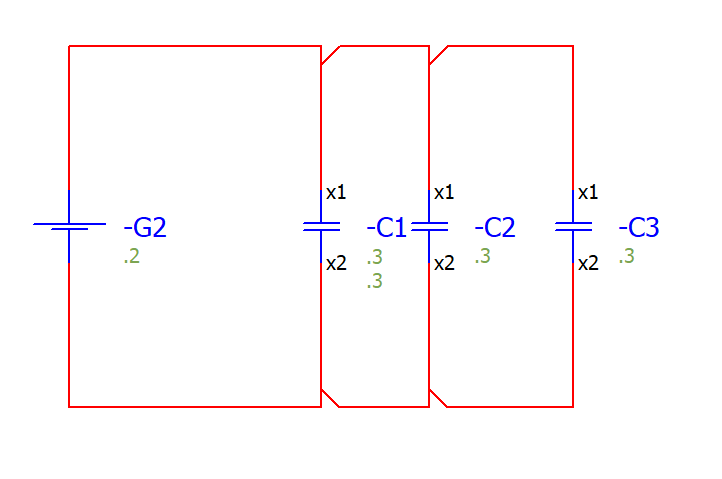
C1, C2, C3 .... 쭉쭉 붙여나갈수록

+가 위치할 수 있는 공간이 늘어나고

-가 위치할 수 있는 공간이 늘어납니다.

그래서 병렬연결에서 커패시턴스의 관계식은 이렇습니다

C1 + C2 + C3 = C(total)

끝이네요.ㅎ

다음 시간에는 커패시터 만큼 중요한

인덕터라는 소자에 대해서 알아보겠습니다.

즐거운 한주 마무리하세요

오래간만입니다.

개인적으로 2022년 많은 일들이 있어서 오래동안 포스팅을 쉰점

독자 여러분들께 깊은 양해를 구합니다.

바로 포스팅 시작하도록 하겠습니다.

캐패시터는

전기를 마치 저장하는듯 보입니다.

양극판에 모인 양전하와 음전하가 닿을듯 말듯한 거리에서 서로를 인력으로

끌어당기고 있기 때문이라고

지난 포스팅에서 설명드린 바 있죠.

일반적으로 캐패시터가 전기를 저장할 수 있는 이유는

음전하와 양전하가 만날 수 있는 길이 없기 때문입니다.

이게 무슨소리냐.?

그림1을 보자면.

한쪽 극판에는 '+' 가 쌓이고

나머지 다른 극판에는 '-' 가 쌓입니다.

지금까지는 전압원이 큰힘으로 양전하와 음전하를 극판에 모아주었죠.

전압원이 없다면 음전하는 양전하와 만나기위해 다음과 같이 곧장 경로를 틀겠죠.

아래처럼요

근데 전압원이 있다고 했을때 왜 전자는 위 그림처럼 이동하지 않느냐???

전압원이 존재할 경우 음전하가 양전하와 만날 수 없는 이유는

전자가 양전하를 만나려는 힘보다 전압원이 극판으로 밀어내는 힘이 훨씬 강하기 때문이죠.

즉, 엄청나게 큰힘으로 전압원이 밀어주고 있기 때문입니다.

만약 큰힘의 전압원이 사라지고

극판에 모여있는 양전하와 음전하가 서로 만날 수 있는 더 쉬운 방법이 생겼다고 하면, 어떻게 되겠습니까?

그림 2처럼요

전자는 양전하와 만나기 위해 이동할 겁니다. 

그럼 어떻게 되겠습니까?

그림 3처럼 X1 부분에 전자가 몰려서 중성이 되다보니

상대적으로 X2 부분이 양전하가 많이 생기지 않겠습니까?

그럼 어떻게 될까요? 다시, 전하는 반대방향으로 이동하겠죠

이상적인 커패시터는 이렇듯

전자가 끊임없이 충전과 방전을 진행합니다.

이때 중요한건 이겁니다.

전자가 이동하기 때문에 커패시터는 전류와도 관계가 있는데

커패시터와 전류의 관계는 과연 무엇이냐!?

 10년전 기억이라 가물가물 하긴하지만

천천히 되새겨보면

Q = C * V

라는 공식이 있습니다.

여기서

Q는 전하량을 의미하고 C는 커패시턴스 V는 전압입니다.

여기서 한가지 더 짚고 넘어갈게 있는데요.

전하량과 전류의 관계입니다.

전하량을 시간으로 미분한다는 것은 시간과 전하량의 그래프를 그렸을때 기울기와도 같은데

시간 전하량 그래프에서 기울기는 전류를 의미하거든요

반대로 생각하면, 전류를 시간에 대해 적분하면 전하량이 나옵니다.

직관적으로 이해하시면 이해갈겁니다.

전류라는게 전하의 이동을 나타내는 단위이고, 전하의 이동이 얼마만큼의 시간동안 이루어졌느냐를

나타내는 총량이 전하량 Q라고 생각하시면 쉽겠네요.

시간 속도 거리의 개념과도 같습니다. 

1초에 10미터를 달리는 A가 10초를 달렸다고 하면 100m를 달린거죠

1초에 2만큼 움직이는 전하가 10초만큼 지났다 하면 총 20개의 전하가 흘렀겠죠.

이때 1초에 2만큼이라는 게 바로 전류

10초가 시간

20이 전하량입니다.

다시 돌아와서

Q = C * V

양변을 시간으로 미분 하면 다음 관계가 성립합니다

자 이 수식에서 우리가 생각할 수 있는게 뭔지가 레알 중요한데

잘 생각해봅시다

전압이 시간에 따라 일정한게 직류전압이란 얘긴 예전에 이미했을겁니다.

직류에선 전압이 시간이 지나도 전압이 변화하지 않으므로 전류는 0이 될 수 밖에 없어요

왜냐면 직류전압이 dV / dt = 0이거든요

한마디로 커패시터는 직류전압에서는 개방회로로 동작한다는 의미입니다.

"뭐야 그럼 그림 1은 실질적으로 커패시터가 있으나 없으나 전류가 안흐른다는 뜻이네?"

네 맞아요.

흐르지 않습니다.

직류는 시간의 변화에 따른 전압의 변화가 없으므로(실제로는 약간 있습니다. 그래서 미세하게 전류가 흐릅니다.)

전류는 흐르지 않습니다.

하지만 V1을 치워버리는 순간 극판의 +, -는 위에 설명했듯 무한반복 되는겁니다(이상적인 경우)

또중요한거 하나.

커패시터에서 전압은 갑자기 휙바낄 수 없어요.

수식만봐도 얼추 알 수 있죠

전압이 짧은시간내에 휙바뀐다는 것은

전류인 i 가 무한대까지도 갈 수 있다는 뜻 입니다.

전류가 무한대일 수 가 있나요?

네 없습니다.

그런일은 벌어지지 않습니다.

이 2가지를 기억해야됩니다

커패시터는

1. 전압이 갑자기 변하지 않는다.

2. 커패시터는 직류 회로에 대해 개방회로로 동작한다.

오랜만에 티스토리 포스팅을 시작하니

포스팅이 다소 무거워진 느낌입니다.

설명도 쉽게한다고 하는데 의미전달이 제대로 되었는지 모르겟네요.

여튼 다음 포스팅에서 이러한 커패시터들이 직렬 또는 병렬로 연결되었을때

어떠한 계산으로 값이 계산될 수 있는지 알아보도록 하겠습니다.

지난 시간에는 연산증폭기 중

가산증폭기를 공부했었습니다.

차분증폭기는 가산증폭기와 원리가 비슷합니다.

해서 짧게 이번시간 마무리 해보도록 하겠습니다.

가산증폭기가

여러 입력이 존재하는 경우 입력에 가중치를 두어 합산한 값을 출력하는 것이라면

차분증폭기는

두 입력 사이의 차이만큼 증폭하는 기기입니다.

두입력의 차이만큼 증폭한다는 의미는 돌려 표현하면

두입력상 공통적으로 인입되는 신호는 무시하겠다는 의미로 해석하시면 되는데요.

그림을 보겠습니다.

차분증폭기는 이렇게 생겼습니다.

외부에 전압원 두개가 있고

이상적인 연산증폭기를 가정하고 문제를 해석하는 것이기 때문에

양 입력단 전류는 0입니다.

(V1 - Vo) / R1 = (Va - Vo) / R2

라고 쓸수 있겠죠.

또한

(V2 - Vb)/R3 = Vb / R4 입니다.

Va = Vb

이 수식을 잘 정리하면

아래 수식을 얻을 수 있어요.

Vo = {R2(1+R1/R2)}*V2/{R1(1+R3/R4)} - V1* R2/R1

우리가 위 수식에서 알 수 있는 건.

V1 = V2 가 동일하고

R1/R2 = R3/R4

비율이 성립될 때

아래 수식으로 정리될 수 있다는 사실인데

Vo = (R2/R1)*(V2-V1)

정리해보면 V2와 V1의 차이만큼을 R2와 R1의 비율로 출력을 조정할 수 있다 입니다.

예를들어 이런겁니다.

V2 = 6[V]

V1 = 5[V]

R1 = R2

인 경우에는

단순히 뺄셈 계산기의 역할을 수행할겁니다.

허나

V2 = 6[V]

V1 = 5[V]

R2/R1= 0.8 인 경우에는

0.8[V] 출력이 나옵니다.

뺄셈 계산기는 뺄셈 계산긴데

감도를 조정할 수 있다는 겁니다.

어디에 이런게 응용될 수 있을까요??

R2/R1이 가변저항으로써 그 비율이 계속 변할 수 있다고 한다면,

어떤 전압을 넣던

일정한 출력을 내고 싶은 경우가 있어요.

예시에 든것처럼 0.8[V]가 나오게끔 하고싶은데

어떤 이유로

V2가 7[V]

V1이 5[V]

들어갔다면 어떨까요?

R2/R1 비율이 0.8로 동일하다고 했을때

출력은 1.6[V]가 나올겁니다.

허나 R2/R1의 비율이 0.4가 된다면요?

출력은 0.8[V]가 나오겠죠?

즉 입력의 값자체가 통제가 안되고 변하더라도

저항의 비율을 통해서

일정한 출력을 내보낼 수 있다는 의미...!

정전압 소자가 구현되었네요.

지난시간과 다르게 내용 설명이 다소 짧았습니다.

가산기와 감산기는 그 맥락이 같기 때문에

자세한 설명보다는 이상적인 연산증폭기가 이런 원리로 응용되고 있다는 사실을

숙지하실 수 있도록 이글을 작성했습니다.

이로써 이상적인 OP AMP 포스팅을 마치겠습니다.

이 포스팅을 시작하기에 앞서

어떠한 방법으로 이산적인 연산증폭기가

계산에 응용될 수 있는지 말씀드렸었죠.

미분 적분과 같은 고급계산에 대해서 설명하지는 못했지만,

모든 연산수식이 덧셈과 뺄셈에서 이루어지는 것이니 만큼

기초적인 원리를 탄탄히 이해하시고 필드엔지니어로 몸담으신다면

분명 배웠던 것들이 서로 매칭되는 때가 있을겁니다.

안녕하세요.

오랜만에 다시 회로이론 포스팅이네요.

회로이론 포스팅하다가 왜 뜬금없이 반도체 분야를 포스팅했었는지

궁금하셨을수도 있으리라 보는데...

어느날 블로그를 들어와보니 포스팅하겠다고 메뉴는 여러개 만들어 놨었는데

막상 대부분의 메뉴 포스팅이 0이고...

회로이론이랑 PLC만 여럿 있더라고요...

해서 이제는 회로이론뿐만 아니라 중간중간 다른 분야 역시 포스팅을

골고루 해볼까합니다. 

시간이 꽤흘렀지만.

우리는 지난시간에 이상적인 OP AMP에 대해서 공부했었습니다.

이상적이라는 말 자체가

이세상에 없는 소자이지만

이것을 배워야 하는 이유는 분명히 말씀드렸었죠.

이상적인 회로 자체가 소자를 만드는데 목표가 될 수 있기 때문이죠.

아무리 이상적인 회로를 만들기 위해 노력해봤자

이상적인 회로를 만들어낼 순 없을겁니다.

하지만 우린 이걸 만들어내기 위해 노력해야 하는겁니다.

서두가 길었습니다.

오늘은 반전 증폭기에 대해서 배워보겠습니다.

반전증폭기는

이렇게 생겼습니다.

특징이 있다고 하면.

전압원 V2중 '+' 극성을

OP AMP의 - 에 입력시켜주고

접지선을 

OP AMP의 +에 입력시켜줌으로써

실제 출력되는 전압을 역으로 이용하는 결과를 빚습니다

반전 증폭기는 논리회로에서 NOT의 신호를 표현하는 것으로.

1 * (-1) = -1

위 수식에서

(-1)의 역할을 OP AMP가 한다고 보시면 되겠네요.

다시 다른 수식을 보면.

1* (-2.5) =  -2.5

위 수식에서

-2.5가 OP AMP 역할을 하는거니까.

여기서 입력과 출력 전압의 비율이 -2.5인 OP AMP라고 볼 수 있고

Vo/Vi = -2.5라고 볼수도 있겠죠.

OP AMP는 실제의 모습으로 보면

어떤 전압이 들어가면

어떤 출력이 나오는 형식입니다.

회로가 복잡하고 어려워보이지만

사실 반전증폭기의 역할의 주내용은 이게 

끝입니다.

어렵게 수식 계산에 주목하지마세요.

수식 계산이 중요한게 아니라

이게(반전증폭기) 뭐할때쓰는건지 원리를 이해하는게 훨씬 이득입니다.

말씀드렸다시피

연산증폭기는 연산기능을 수행하도록 설계되었습니다.

이쯤 설명했으면 연산기능이 어떠한 원리로 수행되는지

이해하셨으리라 생각합니다.

주내용을 이해하셨으니

부수적으로

수식 계산 역시 진행해보겠습니다.

다시 회로를 들고왔습니다.

이상적인 연산증폭기이니 우리는 아래 사실을 정리할 수 있습니다.

일단

I1 = I2

입니다.

I1 = I2를 옴의법칙으로 정리를 적절히 해보면

(V2 - V1) / R1 = (V1 - Vo) / R2

라는것도 쉽게 이해되시죠?

여기에다가 OP AMP의 단자중 '+'가 접지에 연결되어있으므로

V1이 0[V]가 됩니다.

그말은

V2 / R1 = - Vo / R2

라는 이야기인데

V2라는게 입력 전압 Vi와 같으므로

정리하면

Vi / R1 = - Vo / R2

가되죠.

입력과 출력전압을 정리하면

Vo = -Vi * (R2 / R1)

이라는 의미와 일맥상통하며

Vo / Vi = -(R2 / R1)이므로

여기서 나타낸 -(R2/ R1)이

위에서 열심히 설명한 내용중

아래 인용구

"

1* (-2.5) =  -2.5

위 수식에서

-2.5가 OP AMP 역할을 하는거니까.

"

-2.5를 뜻합니다.

이정도면 이해 못하는게 더힘들거에요.

오늘은 여기까지 하겠습니다.